기초물리학/벡터

스칼라와 벡터

물리량은 기초적인 수준에서 크게 두 가지로 나눌 수 있다. 하나는 양을 가지고 있는 스칼라이고, 하나는 양과 방향을 가지고 있는 벡터이다.

스칼라

스칼라(scalar)는 양만을 가지고 있는 물리량을 말한다. 온도계에서 측정된 온도나, 시계에서 측정되는 시각, 물건의 길이나 그것이 가지고 있는 질량 등이 스칼라 물리량, 스칼라량이다. 물리량을 말할 때 그것의 크기 정보만을 가지고 있으면 스칼라이다.

벡터

반면에 벡터(vector)는 방향도 같이 가지고 있는 물리량을 말한다. 속도를 예시로 들어보자. 자동차가 움직일 때 그것이 움직이는 정도가 있을 것이다. 하지만 그 정도만으로는 자동차가 어디로 움직이는지 알 수가 없다. 따라서 자동차가 어디로 움직이는지에 대한 정보도 있는 편이 좋을 것이다. 이렇게 방향 정보도 같이 적으면 크기 정보만 있는 스칼라가 아닌, 벡터라고 부르게 된다. 벡터를 가지는 물리량은 줄여서 벡터량이라고 부른다.

속도는 방향 정보도 포함하고 있는 벡터이다. 속도에서 방향 정보가 없는 것을 속력이라고 부른다. 따라서 "자동차가 40km/h로 달리고 있다."에서 40km/h는 속도를 말하는 것이 아닌, 속력을 말하고 있는 것이다. 속도로 표현하려면 "자동차가 40km/h로 북서쪽으로 이동중"에서 북서쪽과 같이 방향을 같이 표현해줘야 한다.

스칼라와 벡터

일상생활 속에서는 스칼라와 벡터를 잘 구분하지 않는다. 방향까지 붙여 말하지 않아도 쉽게 전달되는 경우가 많기 때문이다. 하지만, 물리적인 문제를 만났을 때 스칼라와 벡터의 구분은 필요하다. 벡터량이 있으면 그에 대응하는 스칼라량이 반드시 있는 것은 아니지만, 그런 관계에 놓인 눈에 띄는 값들은 몇 가지가 있다.

거리와 변위
속력과 속도
질량과 무게

특히나 질량과 무게는 단순히 방향 정보를 더한 것이 아니다. 질량의 경우에는 크기 정보만 있는 스칼라지만, 무게는 그 질량이 중력에 이끌린 정도를 나타내기 때문에 중력의 방향이라는 방향 정보와 함께 얼마나 이끌려 있느냐를 나타내는 크기 정보도 가지고 있다.

반면에 거리와 변위, 속력과 속도는 방향 정보의 유무에만 차이가 있는 물리량이다. 두 지점이 얼마나 떨어져 있는지를 나타내는 스칼라량이지만, 변위는 한 지점에서 다른 지점까지 어느 방향으로 얼마나 떨어져 있는지를 나타내는 벡터량이다. 따라서 거리와 변위는 방향이 있느냐의 차이가 있을 뿐, 크기 정보는 같다.

벡터를 표현할 때는 보통 화살표를 사용하여 표현한다. 화살표의 머리는 벡터가 가리키는 방향을, 화살표의 길이는 벡터의 크기를 표현한다. 벡터를 쓸 때는 볼드체를 넣거나( ${\mathbf {A}}$ ), 기호 위에 화살표를 넣어서( ${\vec {A}}$ ) 나타낸다.

벡터의 연산

벡터는 네 가지 연산이 정의되어 있다.

스칼라곱
벡터합
내적(inner product)
외적(cross product)

스칼라곱(scalar product)은 벡터에 스칼라를 곱하는 것으로 정의되는 연산으로, 벡터의 크기를 바꾸는 연산이다. 아주 쉽게 말해서 단순하게 숫자(스칼라)를 곱하는 것이다. 즉, 크기가 2인 스칼라를 곱하면 벡터가 두 배가 되고, 크기가 5인 스칼라를 곱하면 벡터가 5배가 되는 것이다. 그래서 때때로 스칼라배(倍)라고 부르기도 한다.

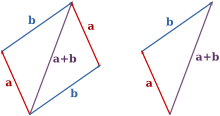
벡터합(vector addition)은 두 벡터의 덧셈으로 정의되는 연산으로, 한 벡터의 머리에 더하고 싶은 벡터의 꼬리를 달아서 총 벡터의 꼬리와 머리를 잇는 벡터를 만든다. 벡터합은 유클리드 공간 상에서 나와있는 벡터에 대해서 벡터의 좌표에서 같은 축에 있는 성분의 합으로 표현된 좌표와 같다. 벡터합을 표현할 때는 +기호로 표현한다. 즉 다음과 같다.

{\vec {A}}+{\vec {B}}={\vec {C}}

유클리드 공간의 좌표로 표현된 벡터에서는 각각의 성분을 서로 더하면 된다. 즉

{\vec {A}}+{\vec {B}}=(a_{1},a_{2})+(b_{1}+b_{2})=(a_{1}+b_{1},a_{2}+b_{2})

이다.

내적(Inner product)은 두 벡터의 곱의 크기로 정의되는 연산으로, 연산의 결과가 스칼라인 연산이다. 내적은 두 벡터 중 하나를 다른 벡터에 사영시켜, 그 크기와 다른 벡터의 크기를 곱한 것으로 볼 수 있다. 다시 말해, 두 벡터의 각도가 $\theta$ 로 주어졌을 때,

|{\vec {A}}||{\vec {B}}|\cos \theta

로 주어진다. 즉, 두 벡터 사이의 각도가 직각이면 내적은 0이고, 90도보다 크면 음수로 주어진다.

내적을 표현하는 연산자는 곱셈을 표현할 때도 자주 쓰는 가운뎃점( $\cdot$ )이다. 즉 내적은

{\vec {A}}\cdot {\vec {B}}=|{\vec {A}}||{\vec {B}}|\cos \theta

이다. 내적에는 중요한 몇 가지 성질이 있다.

${\vec {0}}\cdot {\vec {A}}=0$ ( ${\vec {0}}$ 는 크기가 없는 영벡터(zero-vector))
${\vec {A}}\cdot {\vec {A}}=|{\vec {A}}|^{2}$ (오로지 ${\vec {A}}={\vec {0}}$ 일 때만 ${\vec {A}}\cdot {\vec {A}}=0$ )
${\vec {A}}\cdot {\vec {B}}\leq |{\vec {A}}||{\vec {B}}|$ (코시-슈바르츠 부등식)
유클리드 공간 위의 벡터 ${\vec {A}}=(a_{1},a_{2}),{\vec {B}}=(b_{1},b_{2})$ 가 주어졌을 때 내적 ${\vec {A}}\cdot {\vec {B}}$ 는 $a_{1}\cdot b_{1}+a_{2}\cdot b_{2}$ 으로 주어진다. (쌍대기저가 주어진 힐베르트 공간에서 정의된 벡터 ${\vec {A}}=<A|=<a_{1},a_{2},...,a_{n}|$ , ${\vec {B}}=|B>=|b_{1},b_{2},...,b_{n}>$ 에서 내적 $<A|B>=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n}$ )

4번의 경우 내적을 빠르게 구할 수 있는 방법으로, 몇차원이든 상관없이 유클리드 공간(곡률이 0인 직교좌표공간)에서 유용하다.

외적(또는 가위곱, cross product)은 3차원에서 정의된 벡터의 연산으로 두 벡터의 크기와 함께 방향성을 포함한 연산이다. 외적을 정의하기 위해서는 방향을 정의할 필요가 있다. 외적의 방향성은 xyz좌표에 적힌 축의 순서를 따라가는데, 예컨대 크기가 1이고, 각각 x축, y축, z축에 평행한 벡터 ${\hat {x}}$ , ${\hat {y}}$ , ${\hat {z}}$ 가 있으면 외적 연산자 $\times$ 에 대해서

{\hat {x}}\times {\hat {y}}={\hat {z}}

이다. 내적과는 달리 두 벡터 사이에 각도가 $\theta$ 로 주어져 있으면, 두 벡터의 외적은

{\vec {A}}\times {\vec {B}}=\sin \theta |{\vec {A}}||{\vec {B}}|{\hat {n}}

(여기서 n은 A와 B에 수직이면서, 외적의 방향성을 가지는 크기가 1인 벡터)

으로 나타나, 서로의 각도가 직각일 때 절대값이 제일 크고, 평행하면 0이다.

벡터공간과 벡터의 관계

수학에서 사용하는 벡터와 물리에서 사용하는 벡터는 다르다. 수학에서 사용하는 벡터는 벡터공간 위에 있는 원소로, 벡터공간은 이렇게 정의된다.^[1]

체 $K$ 위의 벡터 공간 $(V,+,\cdot )$ 은 $K$ 에 대한 가군이다. 즉, 다음과 같은 튜플이다.

$V$ 는 집합이다. 이 집합의 원소를 벡터라고 한다.
$+\colon V\times V\to V$ 는 함수이다. 이 연산을 벡터 덧셈이라고 한다.
$\cdot \colon K\times V\to V$ 는 함수이다. 이 연산을 스칼라 곱셈이라고 한다.

이 데이터는 다음과 같은 공리들을 만족시켜야 한다.

$(V,+)$ $(V,+)$ 는 아벨 군을 이룬다. 즉, 다음 성질들이 성립한다.
- (벡터 덧셈의 결합 법칙) 임의의 $u,v,w\in V$ 에 대하여, $(u+v)+w=u+(v+w)$
- (벡터 덧셈의 교환 법칙) 임의의 $u,v\in V$ 에 대하여, $u+v=v+u$
- (벡터 덧셈의 항등원) 임의의 $u\in V$ 에 대하여 $u+0=u$ 인 원소 $0\in V$ 가 존재한다.
- (역원의 존재) 임의의 $u\in V$ 에 대하여, $-u+u=0$ 인 원소 $-u\in V$ 가 존재한다.
$(V,+,\cdot )$ $(V,+,\cdot )$ 는 $K$ $K$ 의 가군을 이룬다. 즉, 다음 성질들이 성립한다.
- 임의의 $a,b\in K$ 및 $v\in V$ 에 대하여, $a\cdot (b\cdot v)=(ab)\cdot v$
- 임의의 $v\in V$ 에 대하여, $1\cdot v=v$ . 여기서 $1\in K$ 는 $K$ 의 곱셈 항등원이다.
- (분배 법칙) 임의의 $a,b\in K$ 및 $u,v\in V$ 에 대하여, $(a+b)\cdot (u+v)=a\cdot u+b\cdot u+a\cdot v+b\cdot v$

위에서 내적과 외적에 대한 이야기는 하나도 없다. 위에서 정의된 연산 $\cdot \colon K\times V\to V$ 는 스칼라곱이다. 이것은 앞서 정의한 스칼라곱과 완벽하게 일치한다.

이는 물리학에서 쓰는 벡터는 완비내적공간(힐베르트 공간)의 원소이고, 또, 수학에서 쓰는 벡터는 그저 공간(벡터공간)의 원소이기 때문에 발생하는 일이다. 기초물리학에서 전혀 신경 쓸 필요가 없지만, 위키백과에서 찾아보다가 저런식의 서술이 등장하면 그냥 수학적으로 잘 정의하고 싶어서 그런 것이다하면서 넘겨버리면 된다. 당신이 완비성이 뭔지 모르고 있더라도, 물리학과의 커리큘럼을 넘기는데 전혀 문제가 없다. 코시열이니 뭐니하는 것도 다 필요없고, 그냥 "아, 그냥 실수에 빈 곳이 없다는 거구나."라고만 넘겨도 상관 없다.

↑ w:벡터 공간

[1] w:벡터 공간

[1]