피타고라스 정리 단원에서는 피타고라스 정리를 이해하고 평면에서 두 점 사이의 거리를 구하는 방법을 다룬다.[ 1]
피타고라스 정리의 증명 오른쪽 그림과 같은 정사각형에서 한 변의 길이는
a
+
b
{\displaystyle a+b}
(
a
+
b
)
2
{\displaystyle (a+b)^{2}}
a
b
2
×
4
{\displaystyle \scriptstyle {\frac {ab}{2}}\times 4}
c
2
{\displaystyle c^{2}}
a
b
2
×
4
+
c
2
{\displaystyle \scriptstyle {\frac {ab}{2}}\times 4+c^{2}}
[ 2]
(
a
+
b
)
2
=
(
a
b
2
×
4
)
+
c
2
{\displaystyle (a+b)^{2}=\left({ab \over 2}\times 4\right)+c^{2}}
⇔
(
a
+
b
)
2
=
2
a
b
+
c
2
{\displaystyle \Leftrightarrow (a+b)^{2}=2ab+c^{2}}
⇔
a
2
+
2
a
b
+
b
2
=
c
2
+
2
a
b
{\displaystyle \Leftrightarrow a^{2}+2ab+b^{2}=c^{2}+2ab}
⇔
a
2
+
b
2
=
c
2
{\displaystyle \Leftrightarrow a^{2}+b^{2}=c^{2}}
위와 같은 직각삼각형에서
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
즉, 직각삼각형의 각 변의 길이를 각각
a
,
b
,
c
{\displaystyle a,b,c}
c
{\displaystyle c}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
피타고라스 정리 (Pythagorean theorem)라고 한다.[ 2] [ 3]
좌표평면에서 두 점
P
(
x
1
,
y
1
)
,
Q
(
x
2
,
y
2
)
{\displaystyle P(x_{1},y_{1}),Q(x_{2},y_{2})}
P
(
x
1
,
y
1
)
{\displaystyle P(x_{1},y_{1})}
x
{\displaystyle x}
Q
(
x
2
,
y
2
)
{\displaystyle Q(x_{2},y_{2})}
y
{\displaystyle y}
R
{\displaystyle R}
P
,
Q
{\displaystyle P,Q}
l
{\displaystyle l}
△
R
P
Q
{\displaystyle \triangle RPQ}
l
{\displaystyle l}
P
R
¯
=
x
2
−
x
1
{\displaystyle {\overline {PR}}=x_{2}-x_{1}}
Q
R
¯
=
y
2
−
y
1
{\displaystyle {\overline {QR}}=y_{2}-y_{1}}
l
,
P
R
¯
,
Q
R
¯
{\displaystyle l,{\overline {PR}},{\overline {QR}}}
[ 4]
l
2
=
P
R
¯
2
+
Q
R
¯
2
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
{\displaystyle {\begin{aligned}l^{2}&={\overline {PR}}^{2}+{\overline {QR}}^{2}\\&=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\end{aligned}}}
⇔
l
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
{\displaystyle \Leftrightarrow l={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}
따라서 좌표평면에서 두 점
P
(
x
1
,
y
1
)
,
Q
(
x
2
,
y
2
)
{\displaystyle P(x_{1},y_{1}),Q(x_{2},y_{2})}
l
{\displaystyle l}
[ 4]
l
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
{\displaystyle l={\sqrt {({x_{2}}-{x_{1}})^{2}+({y_{2}}-{y_{1}})^{2}}}}
삼각형의 세 변의 길이를 각각
a
,
b
,
c
{\displaystyle a,b,c}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
c
{\displaystyle c}
[ 5] [ 6]
△
A
B
C
{\displaystyle \triangle ABC}
B
C
¯
=
a
,
A
C
¯
=
b
,
A
B
¯
=
c
{\displaystyle {\overline {BC}}=a,{\overline {AC}}=b,{\overline {AB}}=c}
[ 5]
∠
C
<
90
∘
{\displaystyle \angle C<90^{\circ }}
a
2
+
b
2
>
c
2
{\displaystyle a^{2}+b^{2}>c^{2}}
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
∠
C
>
90
∘
{\displaystyle \angle C>90^{\circ }}
a
2
+
b
2
<
c
2
{\displaystyle a^{2}+b^{2}<c^{2}}
또한 위의 역도 아래와 같이 성립한다.[ 7]
a
2
+
b
2
>
c
2
{\displaystyle a^{2}+b^{2}>c^{2}}
∠
C
<
90
∘
{\displaystyle \angle C<90^{\circ }}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
a
2
+
b
2
<
c
2
{\displaystyle a^{2}+b^{2}<c^{2}}
∠
C
>
90
∘
{\displaystyle \angle C>90^{\circ }}
가로와 세로의 길이가 각각
a
,
b
{\displaystyle a,b}
l
{\displaystyle l}
l
{\displaystyle l}
[ 8]
l
=
a
2
+
b
2
{\displaystyle l={\sqrt {a^{2}+b^{2}}}}
한 변의 길이가
a
{\displaystyle a}
h
{\displaystyle h}
A
B
C
{\displaystyle ABC}
S
{\displaystyle S}
A
{\displaystyle A}
H
{\displaystyle H}
[ 8]
B
H
¯
2
+
A
H
¯
2
=
A
B
¯
2
{\displaystyle {\overline {BH}}^{2}+{\overline {AH}}^{2}={\overline {AB}}^{2}}
⇔
(
1
2
a
)
2
+
h
2
=
a
2
{\displaystyle \Leftrightarrow \left({1 \over 2}a\right)^{2}+h^{2}=a^{2}}
⇔
h
2
=
a
2
−
(
1
2
a
)
2
=
3
4
a
2
{\displaystyle \Leftrightarrow h^{2}=a^{2}-\left({1 \over 2}a\right)^{2}={3 \over 4}a^{2}}
⇔
h
=
3
4
a
2
=
3
2
a
{\displaystyle \Leftrightarrow h={\sqrt {{3 \over 4}a^{2}}}={{\sqrt {3}} \over 2}a}
S
=
1
2
a
h
=
1
2
×
a
×
3
2
a
2
=
3
4
a
2
{\displaystyle S={1 \over 2}ah={1 \over 2}\times a\times {{\sqrt {3}} \over 2}a^{2}={{\sqrt {3}} \over 4}a^{2}}
두 각의 크기가
45
∘
{\displaystyle 45^{\circ }}
a
,
b
,
c
{\displaystyle a,b,c}
c
{\displaystyle c}
1
:
1
:
2
{\displaystyle 1:1:{\sqrt {2}}}
30
∘
{\displaystyle 30^{\circ }}
60
∘
{\displaystyle 60^{\circ }}
a
,
b
,
c
{\displaystyle a,b,c}
c
{\displaystyle c}
a
<
b
{\displaystyle a<b}
1
:
3
:
2
{\displaystyle 1:{\sqrt {3}}:2}
[ 9]
l
=
a
2
+
b
2
+
c
2
{\displaystyle l={\sqrt {a^{2}+b^{2}+c^{2}}}}
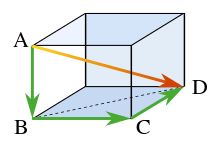
오른쪽 그림과 같은 직육면체가 있을 때 직육면체의 대각선의 길이에 대해 정리하면 아래와 같다.[ 10]
A
D
¯
2
=
A
B
¯
2
+
B
D
¯
2
{\displaystyle {\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BD}}^{2}}
⇔
A
D
¯
2
=
A
B
¯
2
+
B
C
¯
2
+
C
D
¯
2
{\displaystyle \Leftrightarrow {\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BC}}^{2}+{\overline {CD}}^{2}}
⇔
A
D
¯
=
A
B
¯
2
+
B
C
¯
2
+
C
D
¯
2
{\displaystyle \Leftrightarrow {\overline {AD}}={\sqrt {{\overline {AB}}^{2}+{\overline {BC}}^{2}+{\overline {CD}}^{2}}}}
따라서 가로, 세로, 높이의 길이가 각각
a
,
b
,
c
{\displaystyle a,b,c}
l
{\displaystyle l}
l
=
a
2
+
b
2
+
c
2
{\displaystyle l={\sqrt {a^{2}+b^{2}+c^{2}}}}
밑면의 반지름의 길이가
r
{\displaystyle r}
l
{\displaystyle l}
h
{\displaystyle h}
V
{\displaystyle V}
[ 10]
h
2
=
r
2
−
l
2
{\displaystyle h^{2}=r^{2}-l^{2}}
⇔
h
=
l
2
−
r
2
{\displaystyle \Leftrightarrow h={\sqrt {l^{2}-r^{2}}}}
V
=
1
3
π
r
2
h
=
l
2
−
r
2
3
π
r
2
{\displaystyle V={1 \over 3}\pi r^{2}h={{\sqrt {l^{2}-r^{2}}} \over 3}\pi r^{2}}
한 변의 길이가
a
{\displaystyle a}
b
{\displaystyle b}
h
{\displaystyle h}
V
{\displaystyle V}
[ 11]
h
2
=
b
2
−
(
2
2
a
)
2
{\displaystyle h^{2}=b^{2}-\left({{\sqrt {2}} \over 2}a\right)^{2}}
⇔
h
=
b
2
−
a
2
2
{\displaystyle \Leftrightarrow h={\sqrt {b^{2}-{a^{2} \over 2}}}}
V
=
1
3
a
2
h
=
b
2
−
a
2
2
3
a
2
{\displaystyle V={1 \over 3}a^{2}h={{b^{2}-{a^{2} \over 2}} \over 3}a^{2}}
↑ (2011) 《교육과학기술부 고시 제 2011-361호 [별책 8] 수학과 교육과정 》. 대한민국 교육과학기술부, 44쪽 ↑ 2.0 2.1 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 24쪽 ↑ 피타고라스 정리를 증명하는 방법은 본문에서 서술된 방법 외에도 매우 많다. [1] 에서 피타고라스 정비를 증명하는 다양한 방법을 알 수 있다.
↑ 4.0 4.1 장지경. (2007). “좌표평면에서 두 점 사이의 거리 ”. 《Basic 중학생을 위한 수학공식 활용사전》. 신원문화사. ↑ 5.0 5.1 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 28쪽 ↑ 장지경. (2007). “피타고라스의 정리의 역 ”. 《Basic 중학생을 위한 수학공식 활용사전》. 신원문화사. ↑ 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 29쪽 ↑ 8.0 8.1 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 36쪽 ↑ 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 37쪽 ↑ 10.0 10.1 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 41쪽 ↑ 육상국, 윤기원, 이경은, 정석규 (2011). 《EBS TV 중학 수학 3-2 (개념편)》. 한국교육방송공사, 42쪽