쉬운 물리
개요
[+/-]이 책은 물리학을 배워본 적이 없는 사람도 이해할 수 있는 쉬운 물리 책이길 바라면서 쓴다. 수식을 쓰지 않고 물리책을 쓰는 것은 매우 어렵지만[1], 엄밀한 정의를 최대한 건너 뛰고 개념적으로 설명하는 것이 가능하다는 것이 이 책의 철학이다. 얼마나 주저리주저리 늘어지는 책이 될까는 걱정이 되지만 최대한 쉬운 이해가 어떤 것인가 고민해보기로 하자.
물리학은 무얼 하나
[+/-]고등학교의 물리 책을 펼치면, 맨 앞페이지부터 나오는 수많은 용어에 질려서 물리학의 세계에 진입하기 힘들다. 속력, 속도, 변위, 위치... 일상생활에서 접하는 말도 있지만 일본식 한자어를 그대로 들여와서 처음 봤을 때 전혀 감이 안 오는 단어도 있고.
일단은 이런 것을 건너 뛰고 무얼 이야기하고자 하는가를 생각하는 게 낫다.
같이 생각할 수 있는 문제 만들기
[+/-]물리를 한다는 것은 나와 내 주변이 무엇으로 이루어져 있고 어떻게 움직이나를 생각하는 것이다. 내 주변에서 일어나는 일들의 예를 들면, 공 던지기 놀이, 텔레비전, 연못의 파도, 냉장고 같은 것들이 있다.
공 던지기 놀이를 하다 보면 어떻게 해야 공을 세게 던지나, 공이 얼마나 빨리 날아가는가 하는 궁금증이 생긴다. 물리학에서 가장 중요한 질문은 무엇을 알고 싶은가가 아닐까 한다. 물리학은 답이 있는 문제를 생각하는데, 이 때 다른 사람도 똑같은 생각을 할 수 있도록 해야 한다. 어느 정도 '공이 날아간다' 것이 무엇인지 합의가 되어야 한다.
이는 게임의 룰을 정하는 것과 같다. 가령 공 굴리기를 생각해보자. 작은 공이면 별 상관이 없지만 큰 공을 굴리는 시합에서 공의 끝이 결승선을 통과할 때 굴리기가 끝났는지, 아니면 공의 중심이 결승선 통과할 때 끝났는지를 정해야 게임을 할 수 있다.
어떻게 세상을 그릴까
[+/-]먼 옛날, 호랑이가 담배피고, 피타고라스가 삼각형을 그리던 시절, 학문은 그다지 뚜렷하게 분리된 개념은 아니었다. 사실, 물리학과 수학이 분리된 것 역시 그다지 오래된 것이 아니었다. 세상은 여유가 생기면 생길수록, 쌓여가는게 많으면 많을수록 옷장에서 옷을 정리하듯이 많은 것들을 정리하고 싶어한다.
물리학이 다루고자 하는 것은 철학과 그다지 다르지 않다. 세상이 어떻게 이루어져 있고, 세상은 어떻게 움직이는지, 우리 주변에 있는 것들은 어떻게 흐르고, 이 세상 밖에는 무엇이 존재하는지. 세상을 이루고 있는 아주 작은 것에서부터 도저히 헤아릴 수 없는 하늘의 저편까지 세상의 모든 것에 대해서 탐구하는 것이 물리학이다. 특히나 물체의 움직임에 대한 탐구를 하는 것이 물리학이라고 할 수 있다.
현재에 정립된 물리학은 시대의 변화에 따라 점차 엄밀해져 갔지만, 고대에서도 세상의 이치에 대해 궁금한 사람들은 분명히 존재했다. 그들은 자신들이 사는 세계에 대해 나름대로의 합리성을 가지고 세상을 그려나갔다. 우주관이라는 이름으로, 때로는 신화라는 이름으로 만들어낸 여러 문명들의 세상은, 우리 입장에서는 허황된 상상일지도 모른다. 그러나 먼 얘기가 아닌 것이, 이 글을 읽고 있는 독자 중에선 왜 달이 계속해서 떨어지고 있는지 이해하지 못하는 사람들이 많을 것이다. 배가 저편의 바다까지 항해하면 지구의 아래로 떨어지는 것도, 햇님이 밤에는 땅 속으로 숨어들어가는 것도 그 당시 사람들이 관찰하여 얻어낸 지식들 속에서 합리적으로 설명한 것들이었다.
이런 합리적인 설명을 만들어 내는 것이 고대의 물리학이었다. 아리스토텔레스는 고대 그리스부터 유럽의 중세시대까지 물리적인 생각을 각인시킨 사람이었다. 세상을 관찰하면서 얻어낸 것들로 합리적인 설명을 하면서, 우리가 당연하게 여기는 것들의 당위성을 부여하였다. 예를 들어, 아리스토텔레스의 물리학에서는, 움직이는 물체가 멈추는 것은 당연한 것이다. 물체는 그 스스로가 멈출려고 하는 자연적인 성질을 가지고 있기 때문에, 물체는 당연히 멈춰야 하는 것이다. 관성의 발견으로 현대의 물리학도들은 전혀 합리적이라고 생각하지 않는 개념이지만, 우리가 썰매를 타더라도, 이 법칙은 아주 경험적으로 잘 들어맞는다. 굴러다니는 골프공도, 차도, 심지어 미끄러운 얼음 위를 지나는 썰매마저도 시간이 지나면 멈추는데, 자연적인 성질을 가지고 있다는 설명은 굉장히 간결하게 설명할 수 있는 좋은 설명이다.
현대 물리학에서도 간결성은 중요하다. 세상은 그다지 복잡한 것들로 설명되지 않을 것이라는 생각은 여전히 가지고 있다. 태양이 낮에 떠 있는 것도 태양을 갖고 있는 신이 낮에는 땅 위를 움직이고, 밤에는 땅 아래로 움직여서 태양이 떠 있는 것이라는 설명보다는, 지구가 돈다는 설명이 더 간결하다.
정리하자면 물리는 세상을 간결하게 설명해 나가는 것이다.
과학이란
[+/-]과학은 간단히 말하면 과학적 방법을 통해 만들어 낸 지식들의 총본산이다. 좀 더 복잡하게 말하면, 반증가능성을 내포하고 있는 귀납적인 관찰을 과학적 방법으로 검증하여 일정한 법칙들을 쌓아 만드는 지식들의 총본산이다. 과학은 절대적인 신념이 될 수 없으며, 반증을 통해 맞는 것이라 믿어왔던 것이 반박되고 재정립된다.
과학적 방법
[+/-]과학은 자연에서의 관찰을 통해서 규칙들을 발견하고 정립해 나가는 학문이다. 그렇기 때문에 과학 자체는 귀납적이다. 귀납은 관측된 사실을 바탕으로 새로운 지식을 만들어 나가는 논증 방법이다. 예를 들어, "나는 어제 하얀 고니를 보았다."라는 사실이 있고, "나는 오늘 하얀 고니를 보았다."라는 사실과 "너는 그저께 하얀 고니를 보았다."라는 사실이 있다면, 우리는 고니를 보았다면 그것은 하얀색일 것이라고 추측할 수 있을 것이다.
고작 3가지 사실만으로는 충분하지 않을 것이라 생각할 수도 있지만, 이것이 누적되면 고니가 하얀색일 것이다라는 논증은 점점 설득력을 얻게 될 것이다. 더 많은 사람이 더 많은 기간 동안 하얀색 고니만을 보았다면 고니는 하얀색일 것이라는 것이 설득력을 가진다는 것이다. 이것이 귀납이다.
귀납과 반대되는 것은 아니지만 같이 언급되는 논증이 있는데, 연역이 그것이다. 연역은 이미 확인한 사실들을 바탕으로 논리적으로 맞는 추론을 하는 것이다. 대표적인 것이 삼단논법이다. 대전제와 소전제를 바탕으로 결론을 이끌어 내는 것이 삼단논법이다.
대표적인 예시로, 소크라테스는 죽는다라는 결론을 이끌어 내는 유명한 예시가 있다. 사람은 죽는 것이 당연한 일이고(대전제), 소크라테스는 사람이니(소전제), 소크라테서는 죽는 것은 당연하다.(결론)
연역은 귀납과 달리 당연하게 결론을 이끌어낸다. 연역적인 논리체계를 통해서 결론이 타당한지 아닌지를 분명하게 판단할 수 있다. 하지만 연역은 새로운 것을 만들어 내지는 못한다. 삼단논법에서는 대전제와 소전제를 통해 결론을 얻어낼 수 있지만, 대전제와 소전제를 통해 다른 대전제를 이끌어내지는 않는다는 뜻이다.
중학교나 고등학교, 대학교 학부에서 배우는 수학체계는 연역적이다. 전제들이 주어지고, 그 전제들 위에서 여러가지 정리들이 나온다. 그러나 전제들에서 제시한 것들을 바탕으로 만들어 나가기 때문에 전제 외의 것들을 논할 수는 없다.
그러나 과학법칙의 발견은 연역적이지 않다. 자연을 관찰하고 실험하면서 일관성을 찾고, 그것을 일반화하여 법칙을 만드는 것이 과학법칙을 발견하는 과정이고, 과학적 방법이라고 말한다. 이 과정에서 수학과 같은 연역적인 체계를 들고 올 순 있지만, 연역적인 체계가 과학법칙의 본질이 되지 않는다.
과학적 방법은 중세 이슬람문명의 과학자 이븐 알하이삼의 방법론에서 나왔고, 서양의 근대과학을 통해 계승되어 왔다. 정확한 방법론은 없지만, 개략적으로 거치는 과정은 다음과 같다.
- 자연현상에 대한 관찰
- 관찰한 것에 대한 가설제시
- 가설을 증명할 실험의 설계
- 실험의 진행과 검증
- 실험이 실패했다면 2번이나 3번으로 돌아가 오류에 대한 분석, 성공했다면 하나의 데이터로 기록(귀납적인 사례의 축적)
- 재실험 및 결론제시
- 결론에 대한 검증
- (충분한 설득력을 얻었다면)법칙으로 인정
과학적 방법은 가설을 검증하는데 있어서 중요하다. 가설을 제시만 하고 증명할 수 없다면 그것은 과학으로 부를 수 없기 때문이다. 우주 어딘가에 떠돌아 다니는 러셀의 찻주전자처럼 우리가 있는지를 모르는 것을 있다고 말한다면, 없는 것 역시도 있다고 말할 수 있을 것이다. 있을 수도 있지만, 없을 수도 있는 것을 있다고 단정짓는 것은 과학이 아니다. 다시말해, 검증할 수 없는 것은 과학의 영역이 아니다.
반증가능성
[+/-]반증가능성은 러셀의 찻주전자와 마찬가지로 검증할 수 없는 것은 과학의 영역으로 들어가면 안된다는 칼 포퍼의 주장의 핵심이다. 어떠한 사실에 대해서 검증할 수 있는 실험을 설계할 수 없는 가설의 경우, 그 가설은 과학적이지 않다는 것을 내포한다.
반증가능성은 과학과 비과학을 나누는 잣대로 쓰이는 경우가 많다. 검증이 불가능하다는 것은 믿어야 한다는 것인데, 현실에서 일어나는 일들은 믿지 않아도 벌어지는 일들이 있고, 어떤 일이 안 일어난다고 믿는다고 해서 일어나지 않는 것은 아니기 때문이다.
버트런드 러셀의 찻주전자 이야기나 칼 세이건의 보이지 않는 용 등이 비과학을 말할 때의 좋은 예시이다. 우주 어딘가에 돌고 있는 찻주전자를 발견할 수 있는 방법이 있다면 러셀의 찻주전자는 진짜인지 거짓인지 알 수 있고, 보이지 않는 차고에 있다는 불을 내뿜는 용이 자외선 탐지기를 사용해서 있다는 것을 보일 수 있다면 진위를 파악할 수 있겠지만, 그 어떠한 방법을 써도 찾아낼 수 없다면 그것은 과학이 아니라는 것이다.
반증가능성을 내포하고 있다는 것은 이론들이 무너져 내릴 수 있다는 가능성을 가지고 있다는 것을 의미한다. 반례의 등장으로 무너질 수 있다. 가장 대표적인 것이 상대성이론이다. 상대성이론은 1919년에 완성이 된 이론이지만, 검증 자체를 할 수 없었던 이론이었다. 하지만 20년대 30년대가 되고 아인슈타인의 십자가를 발견하고, 우주시대에서 인공위성의 시계가 지구의 시계와 맞지 않다는 것을 발견하면서 기존에 있었던 이론은 무너져 내렸다.
반증가능성은 안타깝게도, 그 말에서 과학의 영역을 내쫓는다. 다중우주설이나 프랙탈 우주, 블랙홀의 내부와 같이 우리의 흥미를 돋구워주고, 과학에 대한 관심을 불러일으켜주는 환상들은 사실 과학이라고 부를 수 없는 상상 속의 이야기이다. 이런 것들은 검증할 수 있는 수단이 없기 때문에 소설과 같은 이야기에 불가능하다.
더 나아가서, 상대성이론이 맞다는 가정하에서 같은 우주라도 관측 가능한 우주 밖의 상호작용하지 않는 우주 마저도 서로 상호작용을 하고 있지 않기 때문에 바깥의 영역은 과학의 대상이 아니다. 빅뱅 이전의 이야기 역시도 마찬가지이다.
그래도 과학의 영역이 아니라는 점은 더 큰 상상력을 제공해준다. 때로는 그 상상력을 통해서 과학의 저변이 확대되는 경우도 있다. 블랙홀이 좋은 예시이다.
블랙홀은 모든 물질들을 빨아들일 정도로 강력한 중력을 가지고 있는 천체이다. 모든 물질이라고 함은, 샤프나 지우개 같은 작은 물체들을 포함해서, 학교나 아파트, 도시 같은 거대한 물체들, 심지어 행성이나 항성들까지도 포함된다. 블랙홀은 사건의 지평선을 지나는 어떤 물체든 빨아들일 수 있는 천체이다. 너무나도 강력해서 빛 마저도 빨아들일 수 있다.
빛 마저도 빨아들일 수 있다면 블랙홀을 볼 수 있을까? 존재를 확인할 수 있을까? 일반적으로는 전혀 알 수 없을 것이다. 우주는 생각보다 어둡고, 밤하늘에서 그런 천체를 찾아보기란 매우 힘들 것이다. 블랙홀과 비슷한 개념인 어둑별을 제시했던 18세기 때만 해도 검증 할 수 있는 방법이 전혀 없었다. 그래도 너무나도 강한 중력을 가진 천체라는 것은 그 자체로 굉장히 매력적인(재미있는) 개념이었다.
이런 vs놀이 같은 상상력은 상대성이론이 나오고 나서도 다시 나왔다. 아주 거대한 밀도를 가지는 천체는 그 자체로 너무 무거워 시공간을 극단적으로 왜곡시키고, 스스로가 붕괴되어 시공간적인 특이점을 만든다는 것이다. SF에서나 나올 것 같고, 조금은 유치해 보일 수 있는 이 개념이 다시 나왔지만, 여러 천체물리학자들이 관심을 가지고, 그것에 대해 다양하게 토론하면서 간접적으로나마 관측할 수 있는 방법을 찾았다.
2017년에 처음으로 사건의 지평선 근처에서 나도는 들뜬 원자가 내놓는 빛을 관측했고,[2] 이것은 그동안 천문학자들이 관심을 가지고 연구했던 블랙홀이라는 천체의 간접적인 발견이었다. 물론 직접적인 관측은 아니지만, 매력적인(재미있는) 상상력을 기초로 쌓아올린 블랙홀 모델을 통한 상상 속의 이야기가 현실로 나타난 사례이다.
모델
[+/-]모델은 여러 이론들로 쌓아올린 것들을 취합해서 새롭게 다른 말이나 형식으로 내놓은 것이다. 이론들을 말할 때 한국어나 영어나 다른 어떤 언어로 표현할 수도 있겠지만, 수식이나 도식 등을 통해서도 표현할 수 있을 것이다. 그 수식이나 도식 혹은 어떠한 형식으로 이론을 표현하고, 다른 이론들 역시도 같은 형식으로 묶어서 어떤 구조를 만들 수 있을 것이다. 이런식으로 이론체계를 다른 무언가로 표현한 구조를 모델이라고 부른다.
판구조론이나 빅뱅이론을 설명하는 도표들이 모델의 좋은 예시이다. 하나의 이론이 아니라 그 동안 쌓아왔던 것들을 적절하게 잘 섞으면서 만든 것이 모델이다. 물리학에서 좋아하는 수학 역시 일종의 모델로 해석할 수 있다.
과학의 특성에 따라 활발하게 연구되고 있는 과학 분야의 경우 모델이 자주 바뀐다. 반증가능성에 따라 항상 모델은 바뀔 준비가 되어있다. 판구조론이 대표적인 예시로, 플룸 구조론이나, 세세한 판의 구분 등으로 모델이 조금씩 수정되어 간다.
패러다임
[+/-]패러다임은 과학적 의식의 총체이다. 사람들이 믿고 있는 체계나 과학 상식등이 패러다임이라고 할 수 있다. 토머스 쿤이 《과학혁명의 구조》[3]에서 처음 언급한 말로, 과학 체계가 뒤집어 지는 것은 단순하게 반례가 생기는 것으로 뒤집어 지는 것이 아니라, 그것들이 축척이 되고 사람들의 인식체계가 바뀌면서 전환되는 비이성적인 과정이라는 것이라 설명한다.
패러다임의 전환의 예시로 천동설과 지동설을 예시를 들었는데, 천동설은 지구는 돌지 않고, 하늘이 움직이고 있다는 것이고, 지동설은 지구가 돌고 있다는 것이다. 현재는 지동설이 더 잘 들어맞는다고 생각하고 있지만, 천동설이 지배적이었을 때는, 천동설만으로도 자연현상이 잘 설명되었다.
천동설은 우주를 지구가 고정되어 있고, 해와 달, 행성들이 원으로 돌고 있다고 설명하는데, 이렇게 설명해서 설명할 수 없는 것은 행성의 역행현상이었다. 천동설에서는 이것을 주전원이라는 개념을 통해서 보강했을 뿐, 천동설 자체를 부정하지 않았다. 이런식으로 어떠한 패러다임에 어긋나는 반례는 그 어긋나는 것을 고치는 식으로 패러다임이 유지가 되었다.
패러다임의 전환은 더 이상 기존의 모델이 반례들을 설명할 수 없을 때 비로소 그 형태를 바꾼다. 지동설의 등장과 튀코 브라헤의 무수한 데이터, 그리고 그것을 바탕으로한 케플러의 3법칙의 등장, 내행성의 위상 문제 등 기존의 패러다임을 흔들만한 새로운 패러다임의 부상으로 패러다임은 새로운 것으로 전환된다.
토머스 쿤은 천동설과 지동설을 예시로 들었는데, 뉴턴의 역학체계와 아이슈타인의 역학체계도 마찬가지이다. 뉴턴의 역학체계에서 태양계 내에 밀도가 균일한 유일한 행성의 경우 태양을 같은 궤도로 타원운동 해야 한다. 하지만 행성들은 세차운동을 한다. 이것을 설명하기 위해 행성간의 중력으로 인한 섭동이 발생한 것과, 행성의 밀도가 균일하지 않고, 어느쪽에는 밀도가 높다는 것을 근거로 세차운동이 발생할 수 있다고 설명했다. 하지만, 그런 복잡한 경우들을 모아서 계산해도 수성의 세차운동을 설명하기에는 오차가 컸다.
1919년에 아이슈타인의 일반 상대성이론은 이런 수성의 세차운동을 설명할 수 있었다. 그러나 일반 상대성이론은 실험적으로 검증하기에는 아직 부족했고, 반증가능성 문단에서 언급했듯이 여러 실제 예시가 나오고 나서야 차츰 받아들여지기 시작했다. 패러다임은 근대에만 전환되는 것이 아니고, 현대에서도 전환이 된다. 그리고, 우주론에서는 아직 풀리지 않는 미스터리들이 나오고 OMG 입자나 아마테라스 입자 등 현대 우주론에서는 설명할 수 없는 초고에너지우주입자(Ultra-High-Energy Cosmic Ray, 줄여서 UHECR)[4]가 검출이 되는 등 패러다임은 지금도 전환될 수 있는 여지를 주고 있다.
물리법칙
[+/-]앞서 언급했듯이, 물리학은 철학과 똑같은 목표를 가지고 있다. 그 중에서 물리학은 물체의 움직임에 대해서 큰 관심이 있다. 물체의 움직임을 언급하기 전에, 우리가 먼저 짚고 넘어가야 할 부분이 있다.
바로 "왜?"라는 질문이다. 4살이나 5살 무렵의 아이들을 만나봤거나, 그 시절의 기억이 남아있다면 "왜?"라는 질문을 많이 하는 것을 봤을 것이다. 사실 진짜 궁금해서 그런 것은 아니겠지만, 일종의 놀이처럼 여기는 것 같아보인다. 그런 질문을 받을 때마다 성실하게 답해주면, 우리는 언젠가 제대로 답해줄 수 없는 상황이 온다. 아마도, 아인슈타인이나 스티븐 호킹이 와도 어떻게 답해줄 수 없는 상황이 온다. 사실 이건 꽤 오랫동안 많은 사람들이 고민해왔었던 주제로, 아리스토텔레스는 그냥 신의 뜻이라고 하면서 넘어갔다.
물리학자들의 생각도 아리스토텔레스와 그다지 다르지 않다. 다만, 그 영향을 아리스토텔레스가 아닌, 에우클레이데스[5]의 영향을 받았다. 에우클레이데스는 원론(기하원론이라는 이명으로도 불린다.)에서 정의와 공준, 공리를 먼저 제시하고 수학적인 해설을 시작한다. 정의와 공준, 공리는 모두 반박금지의 신성한 영역의 무언가이고, 어떤 형태로든 이걸 성공적으로 반박하면, 에우클레이데스가 쌓아올린 원론이라는 이론은 모래성처럼 불쌍하게 무너져내린다.
물리학도 이런 정의, 공준, 공리와 비슷한 원리 혹은 법칙을 내세우면서 이야기를 풀어나간다. 이게 튼튼한 기초인지, 사상누각의 모래들인지는 잘 모르지만, 일단은 이런 물리학을 지탱하는 근본적인 원리에서 시작한다.
시간
[+/-]아리스토텔레스의 물리학에서부터 고전역학, 양자역학과 상대성이론까지 지금 이 순간에도 모두가 받아들이는 한 가지 사실이 있다. 시간은 (한쪽으로)흐른다는 것이다. 시간이 흐르는 이유는 아마 인류가 멸망할 때까지 그 누구도 알 수 없을 것이다. 그만큼 보편적이고, 반박불가능한, 아주 기초적이고 당연한 것이기 때문이다. 시간이 흘러야 한다는 연역적인 정당성은 없지만, 고대부터 지금까지 귀납적으로 흘러왔기 때문에 시간이 흐르는 것은 가장 기본적인 원리이다.[6]
상대성 원리
[+/-]상대성 원리는 모든 물리법칙은 동일하게 적용되어야 한다는 법칙이다. 갈릴레오 갈릴레이가 《두 주요 세계관 관한 대화록》(이탈리아어: Dialogo sopra i due massimi sistemi del mondo)[7][8]에서 주장하였다.
아리스토텔레스의 우주관에서는 천상의 것과 지상의 것은 같은 법칙으로 움직이는 세계가 아니었다. 지상에는 지상의 것이 움직이는 법칙이 있었고, 천상에는 천상의 것이 움직이는 법칙이 있었다. 하지만 천상과 지상의 것이 굳이 다른 법칙을 따를 이유가 없었다. 코페르니쿠스의 지동설이 주장되면서 갈릴레이는 천상과 지상에서 모두 같은 물리법칙이 적용되어야 한다고 생각했었다. 이것은 당연한 생각이었고, 상대성 원리라는 이름으로 물리학에 하나의 가정으로 들어갔다.
상대성 원리는 갈릴레이의 상대성 원리라는 이름으로 불리게 되고, 아인슈타인의 상대성 이론에서 빛의 속력은 일정하다는 가정과 함께 이론의 받침이 되는 원리가 되었다.[9]
근사와 이상화
[+/-]근사
[+/-]물리학에서 아주 잘 쓰는 것 중에 하나가 근사(Approximation)이다. '근사한 꽃이다.'라는 문장에서 쓰이는 대상의 형태를 나타내는 근사가 아니라, '킹크랩은 게에 근사하다.' 같이 쓰일 수 있는 근사이다. 무언가에 가깝게 닮았다라는 의미가 담겨있는 단어이다.
근사는 물리학에서 잘 쓰이는 개념이다. 잘 쓰이는 이유는 사람들이 늘 하는 말 중에 하나인 "이론과 현실은 달라."와 똑같다. 현실에서의 실험들은 이론과 똑같이 나오지 않는다.
카메라로 물건이 떨어지는 낙하실험을 한다고 가정해보자. 일단 카메라를 실험이 진행되는 곳을 찍을 수 있도록 두고, 물건이 떨어지는 순간을 비디오를 담아서 분석하는 것으로 실험을 하자. 이상적인 환경에서는 물건이 떨어지는 모든 지점이 정확히 나와야 할 것이다.
그러나 현실은 그렇지 않다. 일단 우리는 바람을 생각해볼 수 있다. 물건을 떨어뜨리는 순간 바람이 불면 조금이나마 물건이 떨어지는 지점이 예상과는 다른 곳으로 떨어질 수 있다. 또, 우리는 타이밍을 생각해 볼 수 있다. 떨어뜨리라는 지시가 있었지만, 그것을 듣고 실행하는 타이밍이 매번 같을 수는 없을 것이다. 또, 카메라의 성능도 생각해 볼 수 있다. 카메라의 경우 피사체가 카메라로 찍히는 프레임 중앙에서 멀어지면 멀어질수록 왜곡되어 보인다. 지점을 정확히 찍어도 그것이 실제 지점하고 같다는 보장이 없다. 또, 비디오 프레임이 찍히는 시간도 생각해 볼 수 있다. 타이밍을 못 재는 것과 마찬가지로, 비디오가 찍는 프레임 간의 간격이 완벽하게 똑같을 것이라는 보장이 없다.
위와 같은 아주 다양한 이유로 현실의 실험에서는 아주 정확한 값을 찾는 것은 어렵다. 그렇기 때문에 실험을 통해 무언가를 주장을 할 때 쓰이는 것은 여러가지 잡음이 섞인 신호가 아니라, 노이즈캔슬링을 하고 남은 깔끔한 신호이다. 이것을 실험물리학에서는 '피팅'(fitting)이라고 부르지만, 그냥 결론이나 법칙이라고 하자. 실제로 물리법칙들은 아주 정확한 값들을 세세하게 고려해서 나온 법칙이 아니라, 어떤 데이터에서 잡음들만 들어낸 근사한 가정 혹은 경향성에서 나오는 법칙들이다.
물론 이런 것이 정확하다라고 말할 수는 없다. 잡음이라고 하지만, 사실은 어떤 경향성을 나타낼 수도 있고, 실험한 사람들이 측정하지 않은 영역에서 다른 경향성을 띄는 것도 충분히 있을 수 있는 일이다.
그럼에도 불구하고, 근사를 통해서 얻어낸 법칙은 근사한 수준에서는 충분히 좋은 법칙으로 작용한다. 대표적인 것이 뉴턴역학이다. 뉴턴역학은 뉴턴이 쓴 《자연 철학의 수학적 원리》에서 비롯한 법칙들을 바탕으로 발전한 역학체계인데, 20세기 들어서 상대성이론이나 양자역학의 등장으로 사실 전혀 완벽하지 않은 역학체계이다.
완벽하지 않고, 작은 세계나 큰 세계로 갈수록 구멍이 숭숭 뚫리고 있는 역학체계임에도 불구하고, 뉴턴역학은 아주 많은 곳에서 자주 쓰인다. 패러다임이라고도 볼 수 있겠으나, 뉴턴역학은 우리가 사는 세계에서는 아주 잘 들어 맞는다. 설령 근사가 어떤 법칙들을 무시하고 생각하는 것이라고 할지라도, 그 근사가 적용이 되는 세계에서는 그 근사를 통해서 얻어낸 법칙들이 유효하게 쓰인다는 것이다.
이상화
[+/-]이상화(idealization)는 근사와는 달리 이상적인 상황을 가정하는 것이다. 공기저항이나 마찰 등을 무시하는 것이 대표적인 사례인데, 이상화는 모델의 설명을 위해서 잡스러운 것들을 없애는 것이다. 근사는 무시할 수 있을 정도로 작은 잡스러운 것을 제거하여 법칙을 세우는 것이라고 한다면, 이상화는 무시 못 할만한 것이더라도 모델에 대한 설명을 위해서 없애는 것이다. 즉, 그 목적에 따라 쓰이는 것이 다르다.
물리학의 큰 사건들
[+/-]물리학의 역사는 크게 고대그리스, 중세 이슬람, 르네상스, 근대, 현대로 나눌 수 있다. 각각의 시간 속에서 물리학이라는 학문이 생기기도 하고, 크게 바뀌기도 하는 등의 굵직한 사건들이 있었다. 이 사건들 속에는 수 많은 사람들의 이야기가 섞여 있지만, 물리학적으로 큰 족적을 남긴 사람들 위주로 물리학의 역사를 설명할 수 있다.
고대 그리스
[+/-]고대 그리스는 통치력이 아주 쎈 문명이 등장하지 않았다. 하나에 통제된 국가가 없었고, 이데올로기나 제한 등이 그다지 크지 않았던 것을 의미한다. 그래서 고대 그리스에는 다양한 사상가들이 등장할 수 있었고, 다양한 수학적, 물리적인 개념과 실험 역시 등장하였다.[10] 아리스토텔레스나 피타고라스, 유클리드나 에라토스테네스 같은 사람들이 이루어낸 성과들은 그게 옳든 그르든, 수학적, 물리학적인 지평을 늘려나갔다.
그 중 아리스토텔레스의 매력적인 논리는 사람들에게 완벽한 세계관을 주었다. 이 세계관은 중세 유럽까지도 영향력을 미치게 된다. 아리스토텔레스가 주장한 내용은 위키백과의 아리스토텔레스 물리학에 잘 서술되어 있다. 그의 주장은 다음과 같다.
- 천체는 지구를 중심으로 돈다.
- 우주를 구성하는 물질은 총 5가지인데, 지구에서는 4가지의 물질만 존재한다.
- 4가지 물질은 흙, 불, 물, 공기이며, 흙이 가장 무겁고, 물, 공기, 불 순으로 가벼운 성질이 있다.
- 따라서 대지는 흙이 구성하고 있고, 물은 강을 만들거나, 하늘(공기)에서 떨어진다. 불은 공기보다 가벼워 오른다.
- 지구에서 멀리 떨어진 곳에는 인간이 닿을 수 없는 천상의 세계가 존재하며, 천상에는 아이테르라고 하는 물질이 지배한다.
- 별은 수정구 같은 것에 둘러쌓여 있으며, 행성은 수정구 안에서 한 바퀴 돌면서 움직인다.(역행)
기독교의 세계관은 아리스토텔레스의 우주관을 수용하였으며, 기독교가 유럽에 퍼지면서, 기독교에서 수용된 고대 그리스의 철학들을 제외한 나머지 고대 그리스 철학들은 잊혀지게 된다. 로마제국이 멸망하면서 고대 그리스의 서적들은 이슬람 문명으로 번역되어 넘어가게 된다.
중세 이슬람 문명의 황금기
[+/-]현대 이슬람 문명을 바라보는 시선과 달리, 중세 이슬람은 문명적으로 세력, 문화, 학문 전반에 걸쳐 황금기를 맞이한다. 고대 그리스에서 만든 수많은 서적들이 비잔티움 제국의 함락과 함께 이슬람 세계로 넘어와 번역이 된다. 이슬람 문명은 중동을 배경으로한 사막문명으로, 지리적 특성상 무역이 발달하고, 상업이 발달하게 된다. 이에 따라 생기는 상속이나 돈 문제에는 수학이 필요할 수밖에 없었다. 미지수를 사용한 수학은 고대 그리스에서도 쉽게 발견할 수 있지만, 이슬람에서는 유용하게 쓰였다. 대수학을 의미하는 영단어 Algebra 역시 아랍어에서 왔다. 알콰리즈마가 그리스의 수학을 정립하면서 수학을 이끌어왔다.
이슬람교에는 하루에 다섯 번 메카를 향해 절을 해야하는 교리가 있는데, 이 때문에, 무슬림들은 메카가 어느 방향인지를 알아야 했다. 이런 배경은 지구의 기하학적 이해가 필요한 이유가 되었고, 이슬람문명은 고대 그리스의 지식들을 발전시켜 지도제작술을 발전시켰다. 이 시기에 제작한 이슬람 문명의 지도는, 동시대의 다른 문명의 지도보다도 더 정확했고, 다른 문명에서도 이슬람 문명의 학자를 기용하여 지도제작을 부탁하는 일도 생겼다. 무함마드 알이드리시는 당대 인식하고 있던 세계의 지도를 완성시켰다.
이븐 알하이삼의 『광학의 서』도 이슬람 문명의 과학적인 발전을 보여주는 책이다. 특히 이 책은 광학에서의 진전을 보이는 것도 있었지만, 과학적 방법이라고 하는, 실험과학의 바이블과 같은 방법론을 제시했다는 점에서 영향력이 크다.
이외에도 이슬람 문명은 화학이나 역법에 있어서도 큰 성과를 이끌어냈다. 이슬람 문명의 이런 눈부신 발전은 유럽의 가치관의 변화와 함께 유럽으로 흡수되었다.
르네상스와 과학혁명
[+/-]고대 그리스와 중세 유럽은 단절되어 있었다. 과학의 발전보다는 신학의 발전을 중심으로 사회가 돌아갔고, 오컴의 면도날과 장 뷔리당의 관성 실험 외에는 눈에 띄는 발전은 없었다.
르네상스는 한 번에 바뀌어서 구분되는 시대가 아니다. 흑사병의 창궐과 그에 맞물리는 인본주의의 대두, 그리고 중상주의 공화국의 탄생, 인본주의를 찾기 위한 고대 그리스 서적의 번역과 동시에 들어오는 중세이슬람의 학문들 서서히 퍼져나감으로 르네상스가 완성되었다.
피렌체 공화국에서의 메디치 가문은 르네상스를 언급하는데 중요한 부분을 차지하는 가문이다. 로렌초의 후원과 함께 예술문화와 학문이 동시에 발전하면서, 르네상스의 시작을 열었다. 중상주의 공화국들에서의 서적 번역과 전파는 유럽에서의 새로운 학문의 태동이었다.
후원은 특정한 분야의 전문가를 양성하는 바탕이 되었다. 후원으로 갈릴레이가 속해있던 린체이 아카데미나 영국 왕립학회 등 여러 과학단체가 만들어지고, 과학자는 자신의 분야에서 활동할 수 있었다.[11]
우주관의 변화
[+/-]

아리스토텔레스의 아주 합리적이고 아주 틀려먹은 물리학은 르네상스가 다가오면서 위기를 맞게 된다. 아리스토텔레스의 우주관으로 맨 눈으로 관측 가능한 행성들을 잘 디자인해서 태양계(지구계가 더 옳은 표현일지도 모르겠네요.)를 그려보면 위의 그림 같이 나온다. 행성들의 역행을 표현하기 위해서 행성들이 지나가는 자리에 또 원을 그려놓고, 거기에 행성들이 돌아간다는 설명은 보기에도 복잡하다. 또, 다른 행성들에게는 그런 원을 그려놓고 있으면서, 같은 하늘에 있는 달과 태양은 그 원을 갖고 있지 않는지에 대한 설명도 없었다. 이런 배경에서 코페르니쿠스는 저런 그림보다 더 간단한 그림을 만들어냈다. 태양이 중심에 있고, 지구를 비롯한 다른 행성들이 태양을 도는 그림이었다. 지구를 도는 건 달만이 유일한 그림이었다. 이 시대는 광학의 발전으로 망원경이 발명된 시기였다. 망원경은 맨 눈으로는 볼 수 없는 천체를 볼 수 있게 만들어주었다. 갈릴레오 갈릴레이는 망원경을 통해 목성을 관측했고, 맨 눈으로 관측했을 때와 달리 목성의 주위에서 위성이 목성을 중심으로 돌고 있다는 것을 발견했다. 아리스토텔레스의 아주 합리적인 우주관에서는 하늘에 있는 것은 신성한 것이지만, 목성은 지구처럼 위성을 거느리고 있었던 것이다. 즉, 태양을 중심으로 행성이라고 하는 천체들이 돌고, 그 행성을 중심으로 위성이라는 천체들이 도는, 원 안에 원 안에 원이 있는 구조로 모델이 세워진다.

이런 의심스러운 부분에도 불과하고 튀코 브라헤는 아주 완고하게 지구중심설이 옳다고 주장했다. 튀코 브라헤는 아주 뛰어난 천문학자였는데, 튀코는 천체를 관측하는데 있어서 굉장한 정확도를 보여줬다. 튀코는 코페르니쿠스가 태양중심모델을 만들면서 지적했던, 수성과 금성의 최대이각이나 부자연스러운 역행문제를 지구중심설을 살짝 수정한 튀코의 모델로 해결한다. 행성들은 태양을 중심으로 돈다고 하는 모델이었다. 튀코의 모델은 보기에도 괴상한 모델이었다. 정말 말 그대로 태양을 중심으로 지구가 돈다고 말해도 이상하지 않는 모델이었다. 하지만 별은 항상 그 자리에 박혀있다고 생각한다면, 튀코의 모델이 조금 더 합리적이었다. 별을 제처둔다면, 그냥 태양에다가 원 하나 더 그려놓고 지구가 돈다고 말해도 차이가 없는 모델이었다. 해석의 차이에서나 오는 모델이었다. 물론 이 모델은 연주시차의 발견으로 완전히 반박당한다.
한편, 아주 뛰어난 관측실력을 가지고 있는 튀코만큼이나 천문학사에 영향을 준 튀코의 제자가 있었다. 그가 바로 요하네스 케플러로, 케플러는 튀코의 자세한 관측자료를 바탕으로, 태양계를 해석해 세 가지 법칙을 만들게 된다.(이것을 따로 케플러의 3법칙이라고 부른다.)
- 행성은 태양을 한 초점으로 하는 타원 형태로 돈다. (타원궤도법칙)
- 행성과 태양에 가상의 선을 그었을 때, 행성이 어디있든지 상관없이, 행성이 이동한 시간이 같으면 그 선이 쓸고 지나간 면적은 같다.(면적속도일정법칙)
- 행성의 공전주기를 두 번 곱한 것은, 긴 반지름을 세 번 곱한 것과 비례한다.(행성조화법칙)
케플러가 이 법칙을 주장했던 당시에는 사람들에게 외면을 받았다. 하늘은 여전히 신성한 것이었고, 행성이 감히 완벽한 원을 냅두고 타원으로 돈다는 것은 받아들이기 어려웠기 때문이다. 그리고 이 법칙의 증명과정은 반세기 후에 물리학의 역사를 뒤집는 한 물리학자가 자신의 책에 서술하게 된다.
물리학적 개념의 정립
[+/-]
장 뷔리당은 마침내 물체가 사실 멈추려고 한다는 자연적인 본성을 갖고 있지 않다는 주장을 했다. 움직이고 있는 물체는 움직인다고 한 것이다. 이것은 관성이라고 불리는 진짜 자연적인 본성으로 움직이지 않는 것은 움직이지 않으려고 하고, 움직이고 있는 것은 움직이려고 하는 것이다. 갈릴레오 갈릴레이는 사고실험을 통해서 이것을 생각했는데, 마찰이 없는 상태에서 경사면에서 같은 높이로 물체를 굴리고, 그 물체를 각기 다른 각의 경사면으로 올라가게 만들면, 같은 높이로 물체가 올라갈 것이라는 사고실험이었다.(그림) 이것을 좀 더 확장해서 생각해보자. 만약 경사가 지지 않는다면, 물체는 원래 높이를 찾으려고 계속 움직일 것이다. 계속 움직여야 하기 때문에, 물체는 계속 움직이려는 성질을 갖는다. 다만, 갈릴레이도 자연은 완벽하고, 완벽한 것은 원이라는 생각을 가지고 있었기 때문에, 이 관성은 원운동이라고 생각했다. 작은 원이 아니라 무한하게 큰 원이면, 아주 작은 부분에서는 거의 직선에 근사한다. 물론 관성은 원운동에서 나온 것은 아니었다.
철학자(이자 물리학자인) 르네 데카르트는 신의 영원불변성과 접목시키면서 세가지 법칙을 제시한다.[12]
- 모든 물체는 다른 것이 그 상태를 변화시키지 않는 한 똑같은 상태로 남아 있으려고 한다.
- 운동하는 물체는 직선으로 그 운동을 계속하려 한다.
- 운동하는 물체가 자신보다 강한 것에 부딪히면 그 운동을 잃지 않고, 약한 것에 부딪혀서 그것을 움직이게 하면 그것에 준 만큼의 운동을 잃는다.
세 번째 법칙은 보존 법칙과 관련있다. 보존 법칙은 아주 보편적인 법칙 중에 하나다.
우리가 위치를 표현할 때 쓰는 좌표도 근대에 발명 되었다. 직교좌표계라고 하는 좌표체계는 영어로 쓰면 cartesian coordinate(카테시안 코디네이트)이라고 하는데, 이것은 cartes의 좌표 즉, 데카르트(Decartes)의 좌표를 의미한다.
뉴턴
[+/-]위의 내용들을 모두 합쳐, 하나의 책으로 써내려간 사람이 있었다. 그가 바로 뉴턴이다. 대학에 다니고 있을 때 하필 흑사병이 터져 강제 휴학을 하고, 그 와중에 수 많은 이론들을 정립하였다. 뉴턴 나이의 앞자리가 4로 변한지 몇 년 뒤에, 뉴턴은 물리학을 배울 때 반드시 언급되는 그 책을 쓴다. 자연 철학의 수학적 원리(PHILOSOPIAE NATUNALIS PRINCIPIA MATHEMATICA, 줄여서 프린키피아)로 그 안의 있는 내용은 말 그대로 물리학을 다시 썼다는 평가를 받는다. 오늘날, 고전역학이라고 불리는 역학체계는 그냥 뉴턴역학과 동일어이다.
뉴턴은 프린키피아에서 세 가지 법칙을 제시한다.
- 물체는 외부 힘이 작용하지 않는 한 일정한 속도로 움직인다. (관성의 법칙)
- 시간에 따라 물체의 운동량이 변화하는 정도는 그 물체에 작용하는 힘과 (크기와 방향에 있어서) 같다. (가속도의 법칙)
- 물체 A가 물체 B에 힘을 가하면, 물체 B는 물체 A에 방향만 반대되는 똑같은 힘을 동시에 가한다. (작용과 반작용의 법칙)
이 세가지 법칙과 유클리드 기하학, 중력을 사용해 물체의 움직임을 기술한다. 그리고 이 체계는 아인슈타인이 특수상대성이론을 발표하기 전까지 물체 운동을 가장 잘 설명하는 모델이었고, 현재도 계속 쓰고 있는, 가장 간결하고, 인간의 스케일에서 근사하게 들어맞는 모델이다.
산업과 전기의 시대
[+/-]근대 사이에는 오일러나 가우스, 르장드르, 베셀 같은 물리학도들을 괴롭히는 무시무시한 사람들이 많이 있지만, 물리학에 큰 영향을 준 것은 전기의 발명이었다. 제임스 와트의 증기기관의 발명과 함께, 패러데이 법칙의 발견은 세상이 돌아가는 방식을 바꿨다고 해도 과언이 아닐 정도로 시대를 바꾸어 놓았다.
증기기관과 산업혁명
[+/-]제임스 와트가 발명한 증기기관은 기존의 인력을 사용한 노동을 기계로 대체하게 되었다. 증기기관은 석탄 같은 연료를 사용해서 물을 데워 증기를 만들고, 그 증기를 통해 일을 하는 장치이다. 증기기관의 발명은 산업혁명을 촉진시킴과 동시에 열역학에 대한 이해를 늘렸다.
열역학에 대한 이해는 통계역학으로 발전하게 된다.
전자기학의 발전
[+/-]패러데이 법칙의 발견은 전기를 다루는데 있어 매우 중요한 역할을 한다. 전기라고 하는 것은 고대에서도 정전기 형태로 이해하고 있었고, 볼타 전지도 법칙이 발견되기 전에 발명되었지만, 전기를 능동적으로 만드는 방법은 패러데이의 법칙으로 가능해졌다. 패러데이의 법칙은 다음과 같다.
시간에 따른 자기장 세기의 변화(자기선속의 변화)는 전기(전류)를 만들어 낸다.
태양광 발전을 제외한 현대의 모든 발전은 패러데이의 법칙을 사용해서 터빈을 돌리는 방식으로 발전한다. 터빈을 돌려 터빈에 연결된 자석을 돌리고, 자석을 둘러싼 코일에서 패러데이의 법칙에 의해 전기를 만들어낸다.
제임스의 증기기관 발명과 함께 이런 형식의 전기 생산은 산업 혁명을 불러왔다. 석탄을 사용하며 발전을 하거나 증기기관을 돌리고, 이것을 통해 노동시간은 밤으로 연장됐으며, 기존에는 상상도 할 수 없었던 생산력을 얻었다. 전기의 안정적인 공급은 현대문명에 들어서게 하는 디딤돌이 되었고, 지금 당신도 이런 바탕의 산물을 통해 이 글을 읽고 있다.
패러데이의 법칙과 반대되는 현상도 존재했다. 자기장이 전기를 만들어낸 것처럼 전기는 자기장을 만들었다. 이를 앙페르 법칙라고 부른다. 앙페르 법칙은 다음과 같다.
전기가 흐르면, 주변에 자기장이 생긴다.
앙페르 법칙은 패러데이의 법칙과 달리 완전하게 구성된 법칙이 아니었고, 맥스웰이 모순점을 찾아 한 가지 내용을 추가한다.
전기가 흐르면, 주변에 자기장이 생긴다. 그리고 전기장의 변화는 자기장을 만든다.
맥스웰은 그러면서 전자기적 내용을 정리하여 방정식들을 줄여나갔는데, 이를 맥스웰의 방정식이라고 한다.
현대와 상대성, 그리고 양자
[+/-]빛
[+/-]자기장의 변화는 전기장을 만들고, 전기장의 변화는 자기장을 만든다. 이 내용을 정리한 맥스웰 방정식을 다시 한 번 정리하면 특이한 결론이 나왔다. 자기장과 전기장이 서로 변화하면 서로를 만들어낸다는 것이다. 이것은 마치 파동처럼 나아가는데 이를 전자기파, 그 중에서 우리는 특별히 특정한 주파수 대역을 빛이라고 한다.
빛은 산업시대의 물리학에서 현대물리학으로 넘어가는 가장 중요한 물리적 실체이자 현상이다. 빛에 대한 이해가 깊어질수록 새로운 국면을 들추게 되었다. 알렉산드리아의 헤론과 같은 사람이 빛의 특성을 분석했었긴 했지만, 현대물리 태동 이전의 빛에 대한 관점은 크게 두 가지로 나뉘었다.
빛의 입자성
[+/-]빛은 직진성을 가진다. 방향성을 가지고, 그 방향으로 계속 날아간다. 따라서 빛은 물결처럼 퍼져나가는 파동이 아니라, 하나의 입자로 보는 것이 타당할 것이다. 그림자가 지는 것 역시도 그림자가 지지 않은 쪽에는 빛의 입자가 닿고, 그림자가 지는 쪽에는 빛의 입자가 닿지 않았기 때문에 발생한 것이다. 이에 대한 관점을 가진 사람은 아이작 뉴턴이 대표적이다.
더 나아가 빛의 입자성을 보여주는 증거들은 현대물리학에서도 충분히 찾아볼 수 있다. 콤프턴 산란이나 광전효과, 태양광 전지 등 빛을 하나의 알갱이로 가정해야 잘 설명할 수 있는 현상들이 양자역학에서 계속 나온다.
빛의 파동성
[+/-]빛은 파동처럼 퍼져나간다. 빛이 반드시 직진성만 가지고 있는 것이 아니고, 작은 슬릿을 통과하면 빛이 직진만 한다는 가정 속에서는 설명할 수 없는 곳에도 빛이 닿게 된다. 이는 빛이 입자가 아니라는 증거이고, 작은 슬릿을 통과한 빛은 새로운 파동을 만들어서 퍼져나간다는 해석이 가능하다. 이에 대한 관점을 가진 사람은 크리스티안 하위헌스가 대표적이다.
하위헌스는 굴절률이 다른 두 물질 표면에서의 굴절과 반사 현상을 파동성을 통해서 설명하였다. 그 외에도 비눗방울의 다양한 색깔들을 설명하는 박막간섭, 항해 때 쓰이는 썬글라스와 스키장의 스노우 고글을 설명하는 편광현상 등은 빛을 알갱이로 취급했을 때는 설명될 수 없고, 파장으로 취급해야 잘 설명할 수 있다.
특수 상대성이론
[+/-]맥스웰 방정식에서 빛에 대한 특이한 점 중 하나는 속력이 일정하는 것이었다. 전기장과 자기장이 서로를 유도하는데, 서로가 나아가는 속력은 일정한 속력 에 고정되어 있었다.
이것은 매우 기이한 일이었다. 갈릴레이가 정립한 상대성 원리에서, 모든 물리적 법칙은 관찰자가 바뀌어도 바뀌지 말아야 했다. 그러니까, 기찻길 옆에서 투수가 야구공을 던지고 있더라도, 타자의 눈에도, 기차를 타고 있던 승객의 눈에도 투수가 야구공을 던진다는 사실은 바뀌지 말아야 하고, 타자의 눈에는 야구공이 투수가 던진 속도만큼 다가오고, 승객의 눈에는 야구공이 기차의 속도만큼 느려진 속도로 움직여야 한다. 그런데, 빛, 더 나아가 전자기파는, 타자의 눈에도, 승객의 눈에도 같은 속도로 움직인다.
이러한 빛의 움직임은 우리의 직관에 대치 된다. 아리스토텔레스의 물리학이 우리의 직관에 잘 들어맞은 것처럼, 우리의 생각이 저 사실에서는 아리스토텔레스의 물리학이 되어버린 것이다. 아인슈타인은 이를 해결하기 위해 맥스웰의 이론을 바꾼게 아닌, 보는 이에 따라 속도가 일정하게 달라진다는 사실을 바꿨다. 이를 새로 세운 것이 특수 상대성이론이다. 특수 상대성이론은 2가지 가정에서 출발한다.
1. 빛은 누가 바라보든지, 빛의 속도로 움직인다.(맥스웰 방정식으로부터 유도) 2. 물리법칙은 어디서든지, 동일하게 적용된다.(상대성 원리)
이 두 가지 가정에서 얻어낸 것은 공간이 절대적이지 않다는 것이다. 모든 것이 상대적이고, 이 곳의 관찰자가 봤을 때도, 저 곳의 관찰자가 봤을 때도 어떤 운동이 가지고 있는 물리량이 같지 않다는 것이다. 2번 가정에 어긋나는 것 같지만, 상대적인 속도로 보면 맞는 말이었다. 현대물리학에서 양대산맥이라고 여겨지는 이론답게 쉽사리 접근하기 힘든 개념이다. 동시에 대중들에게 널리 알려진 이론이기 때문에 여러 역설들이 제시되었다.
일반 상대성이론
[+/-]
위의 특수 상대성 이론은 단 두 가지 가정으로부터 이끌어 낸 이론이었다. 이것은 어떤 현상에 대해서 서로 다른 속도를 가진 두 관찰자가 관측했을 때의 결과에 대해서 논한 것이었다. 일반 상대성 이론은 좀 더 광범위한 것에 대해 다룬다. 특수 상대성 이론의 아이디어를 바탕으로 우리가 있는 공간에 대해서 다시 쓴 것이 일반 상대성 이론이다.
일반 상대성 이론에서 일반이라고 하는 것은, 초등학교 중학교 같이 어떤 단계(특수)를 오르기 위한 전 단계(일반)이 아니라, 일반화라는 개념처럼 더 보편적인 것을 말하는 것이다. 예를 들어 "소크라테스는 죽는다."라는 말은 소크라테스라는 특정한 사람에게 단정짓는 말이므로 특수한 말이지만, "사람은 죽는다."라는 말은 보편적인 사람들에 대해 단정짓는 말이므로 더 일반적이다. 마찬가지로 서로의 움직임으로만 설명하는 특수 상대성이론을 더욱 확장하여 공간에 대해 설명하는 것이 일반 상대성이론이다.
상대성이론의 주된 개념은 시공간이다. 이전 시대까지는 시간과 공간은 온전히 다른 것으로 인식하였고, 공간을 얼마나 쏘다니건 간에 시간에는 전혀 영향을 미치지 못한다고 생각했다. 여러분이 걸어다니건, 로켓을 타고 성간여행을 하건 아무런 상관없이 시계는 언제나 똑같이 흘러간다고 생각했다. 하지만, 특수 상대성이론에서 시간 역시도 상대적이라는 것을 보여줬고, 우주시대에서 위성의 시계가 안 맞는 것을 발견하면서 자연스럽게 증명이 되었다.
상대성이론의 또다른 주된 개념은 에너지이다. 사실 에너지는 실체가 모호한 물리량이었다. 어떤 일을 낼 수 있는 무언가 정도로만 정의를 해놓고, 이것이 어떤 힘으로 바뀐다는 식의 이해만이 있었고, 19세기가 되서야 코리올리와 퐁슬레에 의해서 운동에너지가 이라는 놀라운 사실을 발견한다.(이 문서에서 수식은 중요하지 않다. 그냥 간신히 저 수식을 얻었다는 것에 주목하자.) 에너지를 중점으로 라그랑주가 역학을 다시 쓰고 난 뒤에 일어난 일이다.
더 놀라운 것은 코리올리와 퐁슬레가 열심히 찾은 은 상대성이론에서는 들어맞지 않는다는 것이다. 좀 더 빠르게 움직이려면 코리올리와 퐁슬레가 찾은 값보다 더 많은 에너지가 들어가야 한다. 심지어 상대성이론에서 에너지는 공간과 시간의 관계 마냥 물질과 근본적으로 같다. 코리올리와 퐁슬레가 찾은 에너지는 물질이 갖고 있는 에너지의 일부다. 물질은 그 자체로도 에너지를 가지고 있고, 그것이 속도를 가지면 나오는 에너지 중 느렸을 때(비상대론적)의 값이 그 값이다. 물질 자체가 가지고 있는 에너지는 어디선가 많이 본 그 수식이다.
여기서 는 에너지이고, 은 질량이다. 는 빛의 속도인데, 핵물리학에서는 조그마한 질량이 거대한 에너지로 바뀐다는 놀라운 사실 때문에 중요하지만, 당장 뒤에서 서술할 것들에서는 딱히 중요하지 않다.
이제 에너지와 질량은 교환이 가능한 값이 되었다. 질량을 가지고 있는 물체는 그 본연적으로 에너지를 가지고 있고, 에너지는 그 자체로 질량으로 전환될 수 있다. 이것을 가장 잘 보여주는 것이 빛, 즉 광자다. 광자는 질량을 가지고 있지 않지만, 에너지를 가지고 있다. 에너지를 가지고 있기 때문에 빛을 흡수하면 열로 전환이 된다. 또 상대성 이론에 의하면 빛은 질량으로도 전환할 수 있게 된다. 이것에 대해서는 양자장론에서 더 자세히 다룰 것이다.
질량은 에너지고, 에너지는 질량이다. 중력은 질량이 가지고 있는 고유한 힘이라고 알고 있었는데, 이제는 에너지 역시 중력을 가지고 있다. 일반 상대성이론에서는 거기에 더해, 중력은 힘이 아니라고 주장한다.
질량을 가지고 있는 것은 다른 질량을 가지고 있는 것을 끌어당긴다는 것은 뉴턴의 사고방식이다. 일반 상대성이론에서는 질량을 가지고 있는 것, 즉 에너지를 가지고 있는 것은 시공간을 휘게 한다. 중력은 딱딱한 탁자 위에서 염동력을 가지고 서로 끌어당기는 마술쇼가 아니라, 트램펄린 같은 탄성력 있는 곳에서 에너지가 가지는 시공간의 왜곡이다.[13] 이 관점은 상대성이론 이전에 잘 풀리지 않았던 수성의 세차운동을 설명하는 역할을 한다.
상대성이론에서 말하는 것들은 대부분 우리 생활과는 관련이 없다. 왜냐하면 상대성이론에서 말하는 것들은 전부 높은 속도와 거대한 질량을 요구하기 때문이다. 상대성이론은 뉴턴역학의 한계와 비유클리드 공간에 대한 논의가 있었던 19세기 말에 그 씨앗을 들어냈는데, 그동안 상대성이론과 관련된 것들이 크게 논의되지 않았던 것은, 극단적으로 큰 스케일에서 잘 보였기 때문이다. 심지어, 우주선을 쏠 때까지도 크게 주목받지 않았는데, 정말로 우리 생활에서 쉽게 찾아보기 힘들었기 때문에 마치 우리가 우주에 대해서 나오는 이야기들을 듣는 것처럼 별세상 이야기로 들렸기 때문이다.
사람이 서는 곳에 따라 보이는 풍경이 다르다는 말이 있다. 그것처럼 우리가 서는 곳이 달라서 보지 못한 것들도 아직 많이 숨어있을지도 모른다.
흑체복사
[+/-]대장간에서 철을 단조할 때, 화로 안에서 나온 철은 붉은 색으로 달아오르는 것을 매체 등을 통해서 접한 적이 있을 것이다. 식으면 검은 색에 가깝게 보이는 철이 왜 붉은 색을 내는가?
철만이 붉은 색을 내는 것은 아니다. 온도가 뜨거우면 뜨거울수록, 어떤 물질이든 붉은 색을 낸다. 붉은 색이 나오는 것은 물질마다 가지고 있는 특성과는 무관하다.
이를 설명하기 위해 흑체라는 개념을 도입했다. 흑체는 검은 물체라는 뜻으로, 반사율이 0에 수렴하는, 아예 반사를 하지 않는 이상적인 물체를 뜻한다.[14] 반사를 하지 않기 때문에 오는 빛들을 족족이 받고, 에너지를 내뱉지 않으면 온도가 무한히 오를 것이다.
하지만 밴타블랙에게 빛을 계속 준다고 해서 온도가 무한히 오르지 않는다. 주변에 연결된 물체에 열을 주면서 온도를 줄일 수도 있지만, 설령 물체에 연결되어 있지 않더라도 밴타블랙은 똑같은 빛이 지속해서 쏘여지는 환경이라면 일정한 온도까지만 오르고 더 이상은 오르지도, 내려가지도 않을 것이다.
이것을 설명하는 것이 흑체복사이다. 열을 가지고 있는 모든 물체는 그것이 어떠한 물질로 이루어져 있는지에 상관 없이 특정한 온도에서 같은 스펙트럼의 빛을 방출한다는 이론이다. 이것을 설명하는 것은 플랑크 법칙인데, 이 법칙은 통계역학으로 설명이 된다. 더 놀라운 사실은, 세상은 연속적이라는 생각에서 벗어나야 설명할 수 있는 것이다.
양자역학
[+/-]양자역학은 뉴턴이 성립한 뉴턴역학과, 아인슈타인이 만든 상대성이론과는 근본적으로 다른 가정이 깔려있다. 뉴턴역학에서 모든 것은 '자연스럽게' 움직이는데, 예시로 사과가 나무에서 떨어질 때 모든 지점에서 사과의 움직임은 끊임없이 부드럽게 움직인다.
그러나 양자역학에서는 그 자연스럽고 부드러운 현상이 아니라, 뚝뚝 끊기는 듯한 현상을 더 근본에 두고 접근한다. 기차역 플랫폼에는 1번 승강장, 2번 승강장 같이 자연수로 끊기는 승강장이 있을 뿐이지, 9와 3/4 승강장이 있지 않다는 뜻이다.
양자역학은 quantum mechanics를 일어로 번역하고, 그것을 들여온 것인데, 여기서 quanta는 라틴어로 양(量)을 뜻한다. 특정한 양이 존재하고, 그것에 대해서만 자연이 반응하는 것을 담아놓은 것이다.
양자역학의 태동은 19세기 말에서 20세기 초까지의 여러 발견들로 시작되었다. 대표적인 것이 앞서 설명한 흑체복사와 원자의 구조이다. 우리가 원자를 그릴 때 자주 쓰는 러더퍼드의 모형에서는 원자핵 주위를 전자가 궤도운동 하는데, 앞서 빛을 설명할 때 말했듯이, 빛은 전자기파이고, 공교롭게도 전자의 움직임은 전기장의 움직임을 만든다. 따라서 전자가 움직이는 모형에서는, 빛이 반드시 나야한다.
빛은 에너지를 가지고 있고, 전자를 통해서 빛이 나왔다는 것은 에너지 손실을 의미하므로, 전자는 운동량을 잃어 핵으로 빨려들어가야 한다. 물론 현실에서 그렇게 나타나지 않는다. 이런 자가당착의 문제들을 해결하기 위해서는 기존의 뉴턴역학과는 다른 체계의 이론이 필요했다.
양자장론
[+/-]현대에 들어서며 고전역학으로 해결 못할 문제가 생겼다. 그래서 그런 점을 보완하며 만들어진 게 상대성이론과 양자역학이다. 상대성이론은 시간과 공간을 포함해 속도, 질량, 크기 등은 관측자의 상태에 따라서 달라진다는 게 상대성이론이라면 양자역학은 매우 작은 입자는 예측하기가 무척 힘들며 입자는 관측하는 형태에 따라 성질까지 달라진다는, 기존의 상식과는 완전히 다른 게 현대물리학이다.
물리학의 범주
[+/-]궁극적으로, 물리학이 추구하고자 하는 것은 철학과 별반 다른 것이 없다. 세상이 돌아가는 이치가 물리학인 것이다. 다만 그 과정에서 그것을 설명할 때, 과학적으로 설명할 수 있는지 아닌지가 그것을 과학으로 나누느냐 마느냐를 나누는 기준이 된 것이다.
과학의 모든 것을 물리학이라고 말하기엔 또 애매한 문제가 될 수 있다. 물체의 움직임도 물리학이고, 천체의 움직임도 물리학이었다. 빛의 움직임도 물리학이고, 아주 작은 입자의 움직임 마저도 물리학이다. 전기도, 오비탈도 물리학의 일종이고, 금속에서 전기가 흐르는 이유를 설명하는 것 역시 물리학이다. 사회의 움직임조차 시뮬레이션으로 분석할 수도 있다. 어떤 사람들은 물리학의 카테고리는 넓다고 말한다. 심지어 화학을 위시한 자연과학의 모든 것에 물리가 존재한다고 말한다.
으레 다른 학문들이 그렇듯이 물리학을 구분 짓는 것부터가 넌센스하다. 서로 다른 학문들이 각자 개별적으로 동떨어져 발전하지 않았다. 수학과 물리학은 서로에게 영감과 도구가 되어줬고, 화학과 물리학은 서로에게 미시세계에 대한 이해를 넓혀줬다. 학문의 경계는 너무나도 부드럽고, 만지면 사라지는 것이다. 무언가를 딱 잘라 말하지는 못하는 것이다.
우리는 이제 일반적으로 다루는 물리학에 대해서 이야기 해볼 것이다.
에너지
[+/-]우리는 물질세계에 살고 있다. 우리가 보는 모든 것이 물질로 이루어져있고, 그것들이 에너지를 교환하면서 움직인다. 우리는 에너지를 먼저 고려해 볼 수 있다.
에너지원
[+/-]
에너지는 일을 할 수 있는 능력이다. 생물이 움직이는데 필요한 것도 에너지고, 차가 움직이는데도 에너지가 필요하다. 스마트폰이나 선풍기 같은 것도 에너지가 필요하다. 에너지는 사라지는 것이 아니라, 다른 것으로 바뀌어 일을 하게 만든다. 에너지를 받을 때 에너지를 주는 것을 에너지원이라고 부르고, ATP나 휘발유, 전기 등이 이런 에너지원에 속한다. 물리학에서 먼저 고려되는 건, 화학에너지나 전기에너지가 아니라 역학적 에너지다.
역학적 에너지와 보존 법칙
[+/-]언덕 위에 공을 하나 생각해보자. 공은 언덕 위에 있으므로, 다른 곳보다 더 높은 위치에 존재한다. 만약 이 공을 조그마한 힘을 줘서 굴리면, 공은 낮은 위치로 이동하면서 동시에 더 빨라진 빠르기으로 움직일 것이다. 물리학에서 이것을 공의 위치 에너지가 공의 운동 에너지로 바뀐다고 해석한다. 위치 에너지와 운동 에너지의 합을 물리학에서 역학적 에너지라고 부른다. 우리는 눈으로 잘 보이는 대상을 예로 들었지만, 다른 에너지원도 크게 보면 위치 에너지를 가졌다고 볼 수 있다.
운동 에너지는 다시 위치 에너지로 바뀔 수 있다. 마찰이나 저항이 하나도 없다는 가정하에서, 어떤 높이에서 멈춰있는 물체가 움직이기 시작하면, 그 높이까지 물체가 움직일 수 있다. 이렇게 위치 에너지와 운동 에너지가 서로 온전하게 바뀌는 것을 역학적 에너지 보존 법칙이라고 부른다. 일상 속에서 마찰이나 저항이 존재하기 때문에 에너지 손실이 바뀌기 하지만,[15] 에너지 보존 법칙은 유효하다. 사라진 에너지는 열 에너지나 소리 에너지 등으로 바뀌게 된다. 이렇게 에너지가 소멸되지 않는 것을 에너지 보존 법칙이라고 부른다. 아직까지 에너지가 보존되지 않는 사례는 존재하지 않는다. 즉, 에너지 보존 법칙은 물리학을 이루는 근본적인 법칙 중 하나다.
역학적 에너지가 보존되는 경우 그 위에서 노는 움직임은 가역적이다. 가역적이라는 말은 어떤 일이 한 원인에서 어떠한 과정으로 발생했을 때, 반대로, 어떤 일을 원인 삼아서 어떠한 과정의 반대 과정을 거치면 그 원인으로 바꿀 수 있다는 것을 말한다. 반대 과정을 거쳐도 원인으로 돌아갈 수 없다면 비가역적이라고 한다. 현실에서 마주치는 대부분 비가역적인 상황이다.
건전지로 움직이는 스케이트 보드를 생각해보자. 스케이트 보드 속의 모터는 전압에 따라 더 빨리 돌기 때문에 많은 건전지를 직렬로 연결하면, 더 빨리 달릴 것이다. 건전지는 위치에너지이다. 건전지(위치에너지)를 더 많이 끼우면, 위치에너지는 운동에너지로 바뀔 준비가 되었고, 스케이트 보드를 출발시키면 위치에너지는 운동에너지로 바뀌어간다. 건전지 속 에너지를 사용해 운동에너지를 얻게 되었다.
하지만 움직이는 스케이트 보드가 멈춘다고 해서 건전지가 충전되지는 않는다. 건전지에 있었던 전력량은 스케이트 보드가 움직이는 동안 소모되었다. 이렇게 어떤 행동에서 역학적 에너지가 보존되지 않는 것을 비가역적이라고 한다.
역학적 에너지가 보존된다면 스케이트 보드가 멈추면 그만큼의 사라진 에너지만큼 충전될 것이다.(실제로 회생제동을 통해 전기차나 전기자전거는 에너지가 충전이 된다.) 그리고 이 환상적인 스케이트 보드를 상상해보자. 에너지가 원래 분만큼 충전되는 스케이트 보드라면 어차피 충전이 가능한데, 건전지(위치에너지)와 잘 탈 수 있는 능력만 충분하다면 충분히 빠르게 달릴 수 있을 것이다. 다만 건전지가 없어도 내리막길에서는 저절로 속도가 붙듯이, 오르막길에서는 건전지가 충전이 되지 않더라도 저절로 속도가 줄어든다. 그래서 더 높은 곳으로 가고 나서 건전지를 확인하면 처음보다 낮은 전력량을 가지고 있을 것이다.
역학적 에너지가 보존된다면 어떠한 경로를 고르든지 한 장소에서 다른 장소로 가는데 드는 에너지는 같다. 학생 A가 집에서 도서관으로 간다고 했을 때, 직선거리로 가든지, 멀리 돌아서 가든지, 급하게 가든지, 느긋하게 가든지 도서관까지 가는데 드는 에너지는 같다. 건전지의 전력량은 집과 도서관의 고도 차이만큼만 날 것이다.
안정 상태
[+/-]
위치에너지는 지형처럼 높은 곳과 낮은 곳이 존재한다. 어떤 곳은 언덕처럼 솟은 곳일 수 있고, 어떤 곳은 웅덩이처럼 움푹 패인 곳일 수도 있다. 웅덩이에 공을 잘 놓으면 공이 안 움직이듯이, 언덕에도 공을 잘 놓으면 공이 안 움직일 것이다. 하지만 공을 살짝 건들이면, 웅덩이에 있는 공은 웅덩이에 머물지만, 언덕에 있는 공은 바로 떨어진다. 이렇게 겉으로는 에너지를 전환하고 있지 않지만, 조그마한 변화에도 금방 다른 에너지로 바뀌는 상태를 불안정하다고 한다. 별이 만들어지는 가설 중 하나인 성운설에서 별의 씨앗이 되는 분자구름이 이러한 상태이다. 반대로, 웅덩이에 있는 공처럼 변화가 있어도 줄곧 웅덩이쪽으로 이동하는 경우 안정적이라고 말한다. 또, 어느 정도는 변화가 있어도 안정적인 상태를 유지하지만, 조금 더 큰 변화가 있으면 위치 에너지가 다른 에너지로 바뀌는 상태를 준안정상태라고 말한다.
사실, 우리가 지금 안정 상태인지 준안정상태인지 알 수 없다. 양자장론으로 다뤄지는 가설 중에서는 초기우주에서 인플라톤(inflaton)으로 이루어진 장이 존재했고, 이것이 인플레이션과 함께 준안정상태에서 벗어나면서 현재의 우주가 생겼다는 가설이 있다. 인플라톤의 시대에서는 가장 낮은 위치에너지가 현재의 가장 낮은 위치에너지보다 높은데, 이는 우리가 알고 있는 가장 낮은 위치에너지가 진짜로 낮은 위치에너지가 아닐 수도 있다. 이를 가짜진공이라고 부르고, 현재 우주도 바닥보다 더 바닥이 있을 것이라고 추측하는 종말론이 존재한다.[16]
모든 물체는 안정적인 상태로 가려고 한다. 이것은 반박할 수 없는 신성불가침의 원리이다. 심지어 너무 기본적이어서 물리학자들이 딱히 이름을 붙이지도 않았다. 물체는 가장 낮은 위치 에너지를 찾아나선다는 소리인데, 사실 위치 에너지가 이런 원리를 바탕으로 기술된다.
최소작용의 원리
[+/-]라그랑주 역학에서 언덕에 있던 공이 웅덩이로 들어갈 때, 처음 공의 위치가 완벽하게 똑같으면 똑같은 경로를 따라 움직인다. 이것은 액션(Action)이라고 하는 물리량이 최소로 하는 경로가 그것이기 때문이다. 이것을 최소작용의 원리이라고 하는데, 빛은 항상 짧은 시간이 되는 경로로 이동한다고 하는 페르마의 원리도 이 법칙의 일종이다. 빛이 경로를 선택할 때 가장 짧은 시간에 닿는 경로를 선택하는 것이 이 최소작용법칙 때문이다. 따라서 아무런 장애물이 없는 경우, 빛은 직선으로 이동한다.
원리에 대한 요약
[+/-]에너지는 일을 할 수 있는 물리량이다. 에너지는 라그랑주 역학에서 아주 근본적인 물리량이고, 에너지에서는 다음과 같은 원리들이 들어가 있다.
- 에너지 보존 법칙: 에너지는 손실되지 않는다. 에너지는 다른 형태로 바뀔 뿐이다.
- 물체는 안정적인 상태로 가려고 한다. 즉 위치 에너지가 낮아지는 방향으로 움직인다.
- 최소작용의 원리: 물체가 움직일 때 액션을 최소화 하는 경로로 움직인다.
운동
[+/-]운동은 일상 속에서 사용하는 단어와는 개념이 다르다. 일상 생활에서는 근육을 키우거나 건강을 유지하는 것에 초점을 두지만, 물리학에서의 운동은 움직임에 초점을 둔다.
단위
[+/-]우리가 어떤 것의 길이를 물어볼 때 신체를 이용해서 답하는 경우가 종종 있다. 한 뼘 정도는 된다, 내 머리보다 크다 등 단위를 잴 수 있는 도구가 없거나 쓰기 귀찮을 때 사용한다. 하지만, 이건 어림잡아 말할 때 유효하지, 제대로 된 기준을 잡을 때 쓰기에는 곤란하다.
단위 치는 원래 손가락 마디 1개를 의미하는 단위이다. 하지만 사람마다 손가락의 길이는 다르기 때문에, 어떤 물건의 길이를 잴 때 치라는 단위를 사용한다면 재는 사람마다 서로 말하는 길이가 달라질 것이다. 잴 때마다 물체의 크기나 지나간 거리가 달라진다면 어떤 물리법칙이든 확인하기 어려울 것이다. 그래서 물리학에서는 모두가 물체를 똑같이 잴 수 있는 통일된 단위가 중요하다.
국제도량형총회는 SI단위계라고 하는 통일된 단위계를 제시했다. 1초나 1m, 1kg 등을 엄밀한 방식으로(일반적으로 알아듣기도 어려운 방식으로) 정의를 했다. 옛날에는 원기라는 실제하는 물건을 사용하여 정의를 했지만, 오늘날에는 이런 방식을 사용하지 않는다. 국제도량형총회에서 제시한 기준들은 오늘날 여러곳에서 사용되고 있고, 우리가 쉽게 찾을 수 있는 자도 이 단위에 맞춰 만들어졌다.
좌표계
[+/-]
단위가 정해졌으니 이제 물체의 위치를 고려해보자. 물체를 표현하기 위해서 크게 두 가지 방법을 생각해 볼 수 있을 것이다. 첫번째는 나를 중심으로 표현하는 방법으로 물체가 존재하는 방향과 물체와 나의 거리를 측정하는 방법이다. 방향은 각도로 표현할 수 있는데, 아주 잘 정의된 도(°)를 사용할 수 있을 것이다. 어느 한 선을 기준으로 잡고, 그 선과 물체의 방향이 이루는 각도를 찾아 각도를 정할 수 있다. 이것을 우리는 극좌표계라고 부른다.
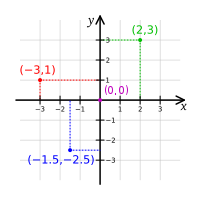
또 다른 방법으로는, 어느 한 직선을 기준으로 직각된 직선을 그리고, 두 직선에 눈금을 표시해 사용할 수 있다. 이것을 우리는 직교좌표계라고 부른다. 나의 입장에서 생각했을 때는 극좌표계가 표시하기 유리하다. 하지만, 운동을 표현하는데 있어서 극좌표계보다는 직교좌표계를 선호한다.
나를 중심으로 좌표를 기술했을 때, 물체가 직선으로 움직일 때의 운동과 우리가 느끼는 괴리감이 크기 때문에 직선 운동에서는 직교좌표계가 유리하다. 이건 차를 타고 갈 때 창밖의 풍경을 보면 알 수 있다. 창문으로 보이는 산이나 바다 같은 멀리 있는 배경은 천천히 움직이지만, 도로의 노란선, 하얀선이나 중앙분리대는 매우 빠르게 움직이는 것처럼 보인다. 사실 움직이고 있는 건 차이기 때문에 멈춰있는 도로의 구조물이나 산과 바다는 같은 빠르기로 움직이고 있는 것처럼 보여야 하는데, 도로의 구조물은 가깝고, 산과 바다는 멀리 있어서 같은 빠르기라고 생각하기 쉽지않다. 마찬가지로, 차창에 기대어 중앙분리대를 바라보면, 멀리있는 것은 어떤 것인지 보기 쉬운데, 가까이 있는 것은 너무 빨리지나가서 보는 것이 쉽지 않다. 따라서 물체의 운동을 기술할 때는 직교좌표계를 사용할 것이다.
물체의 운동
[+/-]물체가 움직이는데 반드시 바뀌는 것은 사실 위치만 있는 것이 아니다. 시각 역시 반드시 바뀌게 된다. 사실 시간이라는 것이 정확히 무엇인지 아는 사람은 없다고 봐도 무방하지만, 시간을 보통 정의할 때 사건과 사건의 간격으로 정의한다.[17] 물체가 움직이기 전과 후에 위치가 바뀌었으므로, 물체가 어디에 존재한다는 사건 두 개가 나타나 시간의 정의에 부합한다. 다시 말해서, 물체가 움직이면 반드시 시간이 존재한다는 것이다.
시간도 역시 국제도량형총회에서 잘 측정한 단위가 존재하고, 세슘-133의 f4와 f3 오비탈의 에너지 준위 차로 발생할 수 있는 빛의 진동수의 역수로 초를 정의한다. 일상 속에서는 간단하게 오차가 적은 쿼츠 시계를 사용할 수 있다.
물체의 운동에서 한 위치에서 다른 위치로 갈 때 텔레포트나 이상한 마법을 통해서 움직이지 않는다. 물체는 자연스럽게 그 위치 사이의 경로를 지나가면서 이동을 하고, 여기에서 물체의 운동에는 위치와 함께 움직이는 정도(빠르기)도 확인할 수 있다. 우리는 이 빠르기를 방향과 합쳐서 속도라고 부른다. 속도는 다음과 같이 정의된다.
속도=(위치의 변화)/시간
예를 들어 민겸이가 집에서 직선거리로 4km 떨어진 도서관을 1시간을 걸어 도착했다면, 민겸이가 집에서 도서관으로 간 사건에서 민겸이는 집에서 도서관 방향으로 4km/h의 속도로 움직인 것이다. 만약에 민겸이가 딴길로 세다가 2시간에 걸어 도착했다면, 사건에서 민겸이의 속도는 집에서 도서관 방향으로 2km/h인 것이다.
조금 이상하게 들릴 수 있지만, 위의 결과는 초기 값과 결과 값을 고려해서 나온 결론이다. 실제로 민겸이가 매 순간마다 4km/h로 걷지 않았을 수도 있고, 8km/h로 달리는 대신 8km의 길을 택했을수도 있다. 하지만 그럼에도 불구하고, 민겸이가 집에서 도서관으로 간 사건에 대해서는 민겸이의 속도는 집에서 도서관 방향으로 4km/h이다.
우리는 이렇게 초기 값과 결과 값만을 고려한 것을 평균 속도라고 부른다. 민겸이가 인도로 걸어갔든, 정글 속을 해쳐나오든 간에 평균적으로 집에서 도서관 방향으로 4km/h의 속도로 움직였기 때문이다. 반면에, 민겸이가 8km/h를 달린 순간을 말할 때는 방향을 말하지 않았을 때는 순간 속력, 방향을 같이 말했을 때는 순간 속도라고 부른다.
물리학자들은 방향이 존재하는지 않는지를 까다롭게 보기 때문에, 속력과 속도는 항상 구분된 개념이다. 방향이 존재하지 않고, 값만 존재하는 것을 스칼라라고 부르고, 방향도 존재하는 것을 벡터라고 부른다. 벡터는 쉽게 말해서, 그 위치에 서서 다른 위치를 바라봤을 때, 그 위치의 거리와 함께 어느 방향으로 시선이 향했는지를 말하는 것이다. 그래서 위치의 변화도 방향을 포함하는 벡터이다.
가(加)속도
[+/-]사실 물체의 운동에서 한 위치에서 다른 위치로 갈 때 텔레포트를 한 게 아닌 것처럼, 물체의 속도 역시 부스터라도 단 것처럼 갑작스럽게 오르진 않을 것이다. 또 속도가 (시간에 따라)변하는 정도 역시 존재할 것이다. 이것을 속도가 더해지거나(加) 줄어지는 물리량이라고 해서 가속도라고 부른다. 이것도 속도처럼 정의할 수 있다.
가속도=(속도의 변화)/시간
왜 이런 걸 알려주는지 의문을 가질 수 있다. 하지만 이 가속도를 통해서 우리가 처음에 다루었던 에너지를 기술할 수 있기 때문에 중요하다. 사실, 라그랑주 역학에서 에너지가 아주 근본적인 물리량인 것처럼, 가속도와 관련된 어느 물리량 역시 뉴턴역학에서 아주 근본적인 물리량이다.
가속도는 눈으로 보기 어려운 물리량이다. 속도는 눈에 띄지만, 속도가 변하는 정도를 알라고 하는 것은 어려운 일이다. 하지만, 우리의 일상생활 속에서 가속도는 작용하는 반대방향으로 쉽게 느끼고 있다.
버스를 타다보면, 버스가 움직일 때 몸이 뒤나 앞으로 쏠리는 경험을 한 적이 많을 것이다. 이는 관성의 법칙에 의해 생기는 것인데, 여기에서 그보다 중요한 건, 그런 경험을 한 순간이 언제인지를 생각해보는 것이다. 아마 버스가 움직이기 시작하면 몸이 뒤로 쏠리고, 버스가 멈출 때 몸이 앞으로 쏠렸을 것이다. 멈춰있는 버스는 가만히 있기 때문에 속도가 0이지만 움직이기 시작하면 속도가 앞을 향해 증가할 것이다. 가속도는 속도의 변화를 시간으로 나눈 값이므로, 가속도도 앞을 향해 증가한다. 우리는 이 가속도를 크기는 같고, 방향만 반대인 쪽으로 느낀다. 그래서 우리는 가속도를 뒤로 증가하는 것으로 느낀다. 그리고 버스가 멈출 때는 속도가 뒤를 향해 증가하므로, 가속도도 뒤를 향해 증가한다. 그래서 우리는 가속도가 앞으로 증가하는 것을 느낀다.
가가속도?
[+/-]위치에서 속도, 속도에서 가속도로 넘어간 것처럼 또 가속도는 갑자기 나온 것은 아닐 것이다. 가속도도 무슨 변화에 있어서 천천히 올라갔을 것이고, 그것을 또 무슨 물리량으로 정할 수 있을 것이다. 그것이 바로 가가속도(jerk)다. 그리고 또, 똑같은 방식으로 가가가속도를 생각할 수도 있고, 그리고 또또, 똑같은 방식으로 가가가가속도도 생각할 수 있을 것이다. 당연하게도 이런 것들은 정의 가능하고, 정의해놨다. 하지만 안타깝게도 물리학자들 관심에는 벗어난 물리량이다.
가가속도까지는 일반적으로 관심을 가질 수 있는 물리량이다. 버스를 타거나 누구의 차를 탔을 때 사람들마다, 차종마다 제각기 다른 승차감을 느꼈을 것이다. 아주 편안하게 패달을 밟아서 속도를 올리는 사람이 있는 반면, 급하게 패달을 밟아서 속도를 올리는 사람도 있을 것이다. 가끔식은 급정거를 위해서 패달을 세게 밟기도 하고, 흥분한 상태로 운전하느라 급발진을 하는 경우도 있을 것이다. 이 때 느끼는 승차감은 가가속도와 관련이 있다. 가속도에서 말했듯이, 우리는 가속도는 자동차가 갖는 가속도의 반대방향으로 느낀다. 쏠리는 정도가 가속도인데, 이게 천천히 쏠리느냐 빨리 쏠리느냐를 가가속도가 결정을 한다. 따라서, 아주 편안하게 운전하는 사람이 있다면, 이 사람은 가가속도를 잘 쓰는 사람으로 볼 수 있다.
단위와 차원
[+/-]물리량은 어떤 물리량을 선택하느냐에 따라 그 물리량이 가지는 단위가 다르다. 속력은 거리/시간으로 나타냈지만, 빛의 세기 같은 걸 생각해보면, 다른 단위를 도입해야 한다. 또 전력은 와트(W)로 사용하고, 전압은 볼트(V)로 사용한다. 물리량은 제각기 다른 단위를 가지고 있다. 두 물리량 비교할 때는 반드시 이 단위를 맞춰줘야 비교가 가능하다.
보통 물리학자들이 물리량을 말할 때 차원이라는 말도 사용한다. 차원은 1차원, 2차원, 3차원할 때 쓰는 차원과 같은 말이고 같은 의미로 사용하지만 무엇에 대한 1차원인지, 어떤 단위들이 결합한 차원인지를 생각하면서 사용한다. 어찌보면 단위와 동의어로 사용하지만, 그 철학적인 의미가 무엇인지 생각해보면 재밌는 상상을 해 볼 수 있을 것이다.
변화량
[+/-]물리학에서 다루는 물리량에는 어떠한 개념을 말하는 것도 있지만, 그것이 어떤 물리량에 따라 변하는 정도를 다루는 물리량인 경우도 많다. 위에서 말한 속도와 가속도는 각각 시간에 따른 위치의 변화량, 시간에 따른 속도의 변화량이다. 비단 시간 뿐만 아니라 위치의 변화에 따른 변화량 역시도 하나의 물리량으로 잡을 수 있고, 에너지의 변화에 따른 물리량도 정의할 수 있다. 변화량의 단위는 관심있는 변화하는 물리량이 분자 쪽에, 물리량을 변화시키려는 물리량이 분모 쪽으로 들어간다. 속도의 단위가 km/h로 나타나는 것도 변화하는 물리량(km)을 변화시키려는 물리량(h)에 따라 어떻게 달라지는지를 봤기 때문이다.
힘
[+/-]
힘은 일상 속에서 아주 자주 쓰이는 표현이지만, 물리학에서 말하는 힘은 단 하나의 의미를 담고 있는 아주 딱딱하고 유도리 없는 개념이다. 힘은(특히나 외부에서 주는 힘은) 물체의 속도를 변하게 하는 것이다. 힘에 대한 정의와 법칙은 아이작 뉴턴이 자연철학의 수학적 원리라는 책에 서술했는데, 이 책은 책이 나오기 이전과 이후로 나뉜다고 해도 과언이 아닐정도로 물리학의 역사에 있어서 아주 중요한 책이다. 아주 중요해서 이 책을 기반으로한 이후의 물리체계를 뉴턴역학으로 불렀다.
각설하고, 뉴턴이 자연철학의 수학적 원리에서 적은 법칙은 다음과 같다.
"운동의 변화는 그것에게 준 힘에 비례하고, 힘이 준 직선 방향으로 영향을 미친다."[18]
즉 힘은 준 방향으로 물체의 속도를 바꾸게 하는 물리량이다. 그리고 뉴턴은 같은 책에서 운동의 양을 속도와 물체의 양을 곱한 값이라고 정의했고,[19] 물체의 양은 또 물체의 밀도를 부피로 곱한 값이라고 정의했었다.[20] 여기서 운동의 양은 운동량이라는 물리량을 말하고, 물체의 양은 질량이라는 물리량을 말한다.[21] 아르키메데스의 유레카로 유명한 일화에서 나오듯이, 부피는 물에 잠기는 물체를 가득 찬 욕조에 담갔을 때 빠져나오는 물의 양과 같고, 밀도는 같은 무게의 물체를 넣었을 때 빠져나오는 부피를 보고 비교할 수 있다.
질량은 무게와 다르다. 무게는 물체의 양이 아니라, 물체가 중력 따위로 갖게 되는 알짜힘이다. 즉, 무게와 질량은 비교가 되지 않는 다른 단위를 갖는 물리량이다.
뉴턴의 법칙에 의하면 힘은 운동의 변화에 비례하는 물리량이다. 그리고 자연철학의 수학적 원리에서 기술된 변화는 암묵적으로 시간에 대한 변화를 나타내기 때문에 이를 수식을 이용해서 표현하면 다음과 같다.
힘=(운동량의 변화)/시간=(질량×속도의 변화)/시간
질량이 변하지 않는 경우에는 질량의 변화가 없기 때문에 힘은 가속도의 정의에 의하여
힘=질량×가속도
로 나오게 된다.[22] 즉, 질량이 변하지 않는 경우에 힘은 질량과 가속도의 곱으로 나타난다. 다시 말해서, 물체의 속도가 달라지는 곳에서는 힘이 존재한다.
뉴턴역학에서 힘은 물체의 운동을 아주 잘 기술하는 가장 중요하고 근본적인 물리량이다. 위에서 에너지가 근본적인 물리량이라고 했지만, 그건 라그랑주 역학에서 통용되는 얘기고, 뉴턴역학에서는 힘이 중요하다.
관성
[+/-]주변에 아무거나 집어서, 바닥에 놓고 밀어보자. 물건은 조금 이동하는가 싶다가도 금방 멈춘다. 고대 그리스의 아리스토텔레스는 물체가 움직임이 멈추는 것은 아주 당연하게 여겼다. 바닥에 물건을 놓고 밀었을 때 금방 멈추는 것처럼, 아리스토텔레스 역시 움직이는 물체는 당연히 시간이 지나면 멈추는 것이 본성이라고 생각했다. 하지만 위에서 살펴봤듯이, 시간이 지나면 멈추는 것은 본성이 아니라 힘이 작용한 것이다.
그럼 힘이 없는 상황에서는 어떻게 되는가? 우리는 위에서 속도가 달라지는 곳에서는 힘이 존재한다고 했다. 다시 말해서, 힘이 존재하지 않으면 속도는 달라지지 말아야 한다는 것이다.
아리스토텔레스 말처럼 움직이는 물체가 멈추는 것이 본성이라면, 우리 지구는 존재할 수 없다. 지구는 태양을 돌고 있고, 태양은 중력에 따라 지구를 당기고 있다. 아리스토텔레스의 주장을 따라가면, 지구의 본성에 따라 지구는 시간이 지나면 태양 주위를 도는 것을 멈춰져야 하고, 이로 인해서 지구는 태양으로 다이빙을 해야 한다.
아리스토텔레스가 주창하던 물리학에서는 지구가 우주의 중심이고, 달, 화성, 수성, 목성, 금성, 토성, 태양[23] 모두 기하학적으로 완벽한 원운동을 하지만, 갈릴레이가 망원경을 발명한 후 튀코 브라헤가 관측한 자료에서 행성은 기하학적으로 완벽한 원운동을 하지 않았고, 갈릴레이의 상대성 원리에 의해 모든 공간에서 물리법칙은 같다. 하늘이라고 다른 법칙이 적용되면 안되고, 땅 속이라고 해서 다른 법칙이 생기는 것이 아니다.

관성이란 힘이 존재하지 않을 때, 그 운동을 계속하려고 하는 것을 말한다. 같은 속도를 유지하기 때문에, 차가 브레이크를 밟을 때 몸이 앞으로 쏠리는 것 역시, 차는 힘을 받고 있는데, 몸은 힘을 받고 있지 않는 상태여서 앞으로 쏠리는 것이다. 시트의 마찰이나, 안전벨트의 탄성이 없다면 몸은 관성 때문에 차 안에서 봤을 때 앞으로 나아갈 것이다.[24] 차 안에서는 마치 몸이 앞으로 힘을 받은 것처럼 보이지만, 차 밖에서 봤을 때는 몸이 그 운동을 계속하고 있는 것이기 때문에, 몸은 관성을 유지하고 있다.
가속도 설명에서 가속도를 반대방향으로 느낀다는 것도 이런 관성의 원리에서 비롯된 것이다. 멈춰있는 차 안에서 앉아있다가 차가 움직이면 뒤로 쏠리는 느낌이 드는 이유는 차 동체가 앞으로 가속하고 있는데 몸은 가만히 있기 때문이다. 차가 가속하면서 차는 차 안에 있는 물체도 밀게 되고, 의자에 앉아있는 사람은 그만큼의 힘을 시트를 통해서 느끼게 된다.
작용 반작용
[+/-]힘은 휘두르는 것이 아니라 같이 나누는 것이다. 물리학에서는 그렇다. 즉, 힘이 작용하면, 그것에 정확히 반대되는 힘이 작용(반작용)한다. 이것을 작용 반작용 법칙이라고 부른다. 힘은 상호작용적이고, 내가 준 만큼 남에게 받는다.
당구에서 두 당구공을 칠 때 당구공의 움직임이 그 예시이다. 하얀색 당구공으로 멈춰있는 빨간색 당구공을 치면 멈춰있는 빨간공은 하얀공에 의해서 움직여지고, 움직여졌으니까 운동량이 달라졌다. 운동량의 변화는 힘이기 때문에, 하얀공이 빨간공에게 힘을 줬다. 그런데, 하얀공 역시 빨간공을 쳐서 감속을 한다. 이동방향이 조금 바뀌었거나, 멈췄거나, 아예 거꾸로 움직여도 운동량이 바뀌었다는 것은 분명하다. 따라서 하얀공 역시도 힘을 받았다. 만약 당구공이 부딪히는 소리까지 들리지 않았다면(에너지의 손실이 없다면), 빨간공하고 하얀공의 움직임을 측정했을 때, 하얀공이 잃은 운동량을 빨간공이 고스란히 가져간 것을 측정할 수 있다. 이걸 물리학에서 운동량 보존의 법칙이라고 부른다. 운동량 보존의 법칙은 작용 반작용 법칙의 특수한 경우로, 당구공이 부딪히는 소리가 나더라도 작용 반작용 법칙은 그대로 일어난다.
작용 반작용은 법칙이기 때문에 두 물체가 가까이 부딪히는 것뿐만 아니라 멀리 떨어진 물체가 서로 상호작용하는 것 역시 작용 반작용이 일어난다. 중력도 겉으로 보기에는 아주 크고 지배적인 물체가 아주 자그마한 물체를 잡아 당기는 것처럼 보이지만, 사실 자그마한 물체 역시 거대한 물체를 잡아당긴다. 그렇기 때문에 지구와 달은 서로가 서로를 돌고 있으며, 돌고 있는 점은 지구의 정중앙이 아닌, 지구의 정중앙에서 살짝 벗어난 곳에 위치하고 있다.
작용 반작용 법칙은 두 물체에 작용하는 힘이 서로의 반대방향으로 상호작용하는 것을 의미하는 것이기 때문에 모든 물리현상은 넓은 계에서 보면 힘이 0인 현상이라는 것을 시사한다.
충돌
[+/-]
때때로 매체에서 묘사할 때, 주인공이나 사람이 땅에 떨어지는 것을 막기 위해서 날고 있는 로봇이나, 생명체가 공중에서 태우는 경우가 있다. 과연 이런식으로 구하면, 사람이 땅에 떨어지는 것보다 나을까?
어떻게 태우냐에 따라 다르다고 말할 수 있다. 태우는 대상이 같이 떨어지면서 태우면 낫다. 그러나, 지표면에 평행하게 날아가면서 태우거나, 상승하면서 태우면 땅에 떨어지는 것보다 못하다. 왜 그럴까?
답은 이미 언급했다. 우리는 갈릴레이의 상대성 원리를 떠올릴 필요가 있다. 상대성 원리가 말하는 것은 보편성이다. 모든 물리법칙은 동일하게 작용해야 한다. 이것은 지면에서도 마찬가지고, 하늘에서도 마찬가지다. 즉, 이것을 생각할 때 고려해야 하는 것은 지면은 위험하다라는 생각이 아니라, 왜 떨어지는 것이 위험하냐는 것이다.
약간은 꺼림직하긴 하지만, 떨어지는 사람을 생각해보자... 아니, 떨어지는 사과를 생각해보자. 사과는 뭐.. 당연히 나무에서 떨어지긴 한다. 그 경우에 사과는 대게는 아무런 생채기도 없이 풀바닥에 떨어질 것이다. 나무보다 높은 경우에는 어떠한가? 아파트 10층 높이에서 콘크리트를 향해 사과를 떨어뜨리면 사과는 아작이 날 것이다. 두 상황에는 어떠한 차이가 있는가?
먼저 높이를 생각해볼 수 있을 것이다. 높은 높이에서 떨어지면, 중력이 작용하고(중력도 힘이다. 따라서 가속도를 줄 것이다.), 그것 때문에 속력이 붙을 것이다. 속력이 붙은 상태에서 바닥에 부딪히면 운동량이 크게 변할 것이고 이 과정에서 물체가 버티지 못하면 파괴될 것이다.
이런 생각은 꽤나 합리적이지만, 그래도 설명하지 못하는 것이 있다. 바닥에 커다란 에어매트가 있으면 사과는 파괴되지 않고 원형을 유지한다. 에어매트리스는 무슨 역할을 하기에 사과가 아작나지 않도록 하는가? 에어매트는 충돌시간을 늘려준다. 충돌시간이 늘어나면 어떻게 되는가?
충돌시간이 길어지면 운동량이 비교적 서서히 줄어든다. 물체에 운동량이 변할 때의 상황을 생각해보면, 충돌하는 부분부터 운동량이 바뀌고, 그것이 마치 파도처럼 충돌부에서 멀어지는 쪽도 운동량이 바뀌는 식으로 진행이 될텐데, 이것이 매우 빠르게 일어나면 물체를 이어주던 힘이 끊기게 될 것이다. 반면에 천천히 일어나서 이어주는 힘이 다시 복원이 될 수 있을 정도만 된다면 물체는 원래 형태를 복원할 것이다.
위에서 뉴턴이 힘을 정의할 때 운동의 양의 (시간적) 변화라고 했다. 즉, 이것을 힘으로 해석할 수 있을 것이다. 따라서 충돌시간이 짧으면 힘이 세지고, 충돌시간이 길어지면 힘은 약해질 것이다.

이 힘을 충격력이라고 한다. 충격력은 충격량과 관련있는데, 평균충격력에 시간을 곱한 값이 충격량이다. 그리고 이 값은 우연히도 (아주 당연하게도)운동량의 변화량과 같다. 또 다시 말해서, 시간이 작으면 작을수록 충격력은 올라간다.
이제 다시 돌아가 땅에 추락하고 있는 사람을 생각해보자. 땅에 떨어지고 있는 사람을 중간에 태우는 것과 차이는 높이에 의해 생기는 속도차일 것이다. 그런데, 대기가 존재하는 높은 곳에서 떨어지면, 속도의 차이를 별로 없다. 대기가 존재하면 공기저항이 존재하고, 공기저항으로 인해 떨어지는 물체는 속력은 종단속력보다는 더 오르지 않는다. 즉, 충분히 높은 곳에서 떨어지면 높은 곳에 떨어지든, 낮은 곳에 떨어지든 받는 충격량은 같다.[25]
따라서 추락하고 있는 사람을 공중에서 받을 때, 상승하거나, 같은 고도를 유지하면서 받으면 그 사람이 받는 충격은 땅에 떨어질 때 받는 충격과 같거나, 더 심할 수도 있다. 물론, 받는 것이 땅바닥보다 (사과의 예시에서 풀바닥처럼)더 푹신푹신한 소재면 충돌시간이 증가하기 때문에 충격력은 더 낮아진다. 그러면 사람을 공중에서 받으려면 어떻게 해야할까?
충격량은 운동량의 변화량과 같다고 위에서 말했다. 다시 말해서, 떨어지는 사람의 운동량의 변화가 적다면 충격량은 줄어든다. 떨어지는 사람의 속도는 아래방향이므로, 운동량 변화를 줄이려면 받는 쪽도 같이 떨어지거나, 적어도 팔을 아래로 내려야 한다.
사실 충격력을 줄이는 것은 일상생활에서 쉽게 찾아볼 수 있다. 충격량은 그대로 둔 상태에서 시간을 늘리면 충격력이 줄어들기 때문에 공 같은 것을 손으로 받을 때, 팔을 뒤로 당기면서 받으면 비교적 손에 충격이 덜한 체로 공을 받는다.
요약
[+/-]물리학을 쓰는데 물체의 운동은 지대한 관심사였다. 라그랑주 역학에서는 물리학을 보는 시선이 바뀌었지만, 물체의 운동은 물리학을 기술하는 것은 그 시대의 흐름에서도 변하지 않고 중요한 것이었다. 물체의 운동을 표현하거나 에너지를 보는데 있어서도 위치는 아주 근본적이고 당연한 것이다. 이 문단에서 표준적인 위치를 기술하는 법을 살펴 보았다.
물리학에서의 변화라고 하는 것은 어떤 것을 논하는데 있어서도 제일 우선 시 되고 너무나도 당연한 것이다. 시간의 흐름이 없으면 우리가 다룰 수 있는 것은 정역학을 제외하고는 어떤 것도 없다. 심지어 정역학도 힘을 다루는 학문이기 때문에 세상의 시간의 흐름이 없으면 쓸모 없는 것이다. 우리는 물체의 운동을 기술하기 위해 위치의 변화량과, 그것의 변화량, 또 그것의 변화량까지 대해 알아보았다.
뉴턴은 물리학사에서 엄청난 변화를 가져온 사람이었다. 뉴턴이 쓴 모든 것이 그의 업적인 것은 아니었으나, 뉴턴이 쓴 것들에 기반해 물리학이 다시 쓰여졌다. 위에서 언급한 관성의 법칙, 힘의 정의, 작용 반작용 법칙은 상대성이론이라는 대격변을 겪었으면서도 여전히 유효한 물리법칙들이다.
차원의 전환
[+/-]이 책은 쉽게 물리를 서술하는 것을 지향하지만, 그래도 물리학을 이해하기 위해선 미분과 적분은 짚고 넘어갈 필요가 있다.
아주 간단하게 말해서 미분은 세세하게 나눈 것에 대해서 표현한 것이고, 적분은 하나하나 쌓은 것이다. 미분은 어떤 현상에 주어진 어떤 차원의 물리량에 대해서, 어떤 단위로 나누어진 차원의 물리량으로 표현할 때 사용하는 계산법이고, 적분은 어떤 단위로 곱해진 차원의 물리량으로 표현할 때 사용하는 계산법이다.[26]
위에서 살펴보았던 속도의 정의(속도=위치의 변화/시간)가 미분에 가까운 개념이다. 정확히는 순간속도가 위치의 미분이다. 속도의 정의를 조금 틀어 위치를 위치=속도×시간이라고 하는 것은 적분에 가깝다. 정확히는 속도의 정의가 위치의 변화였으므로, 위치=속도×시간+원래 위치가 적분이다.
위에서 변화량에 대해서 다루었었다. 뉴턴의 업적 중 하나도 역시 이 변화량에 대한 이야기였으며, 그것이 미적분이다.[27] 미적분은 단순히 미분과 적분을 합쳐 부르는 말이고, 사실 미분은 뉴턴 대에 발명되고 적분은 고대에서부터 존재했지만, 미분과 적분의 관계를 찾아내고 연결시켰기 때문에 미적분이라고 부른다.
적분
[+/-]
적분(積分)은 나누어서(分) 쌓아올린다(積)는 뜻이다. 곱셈이라고 하더니만 왜 나누냐고 생각할 수 있겠지만, 적분이 고대부터 쓰였을 때는 도형의 크기를 알아내는데 사용됐기 때문이다.
원의 넓이를 구할 때 흔히 제시 되는 방법은 오른쪽 그림과 같다. 초등학교 6학년 즈음에 원을 다루면서 나오는 그림인데, 원을 부채꼴로 잘라 직사각형 같이 만들어서 높이와 길이를 곱해서 원의 넓이를 구하는 방법이다. 저 그림에서 부채꼴이 세밀하게 나누어지면 나누어질수록 부채꼴에서 둥근 부분의 곡률이 점점 더 줄어들어 저 방법으로 구하는 원의 넓이가 실제에 가까운 값이 나오게 된다.
버리는 부분이나 채우지 못하는 부분을 최소화 해서 구하고자 하는 도형의 크기를 최대한 가깝게 구하는 것이 적분의 목적이다.
아르키메데스의 원의 넓이
[+/-]
뉴턴이 바꿔놓은 미적분 이전에 적분으로 유명한 예제는 아르키메데스가 생각한 원의 넓이를 구하는 방법일 것이다. 아르키메데스가 생각한 방법은 오른쪽 그림과 같이 우리가 넓이를 잘 아는 도형을 활용한 방법이었다. 삼각형의 넓이는 우리가 잘 알고 있는데다가, 삼각형을 반으로 쪼개도 삼각형이 나오기 때문에, 먼저 정삼각형의 정삼각형을 꼭지점이 원에 닿게 안쪽에 하나, 정삼각형의 변이 원에 닿게 바깥쪽에 하나를 그려놓았다.
추가적으로 설명할 것도 없이, 원의 넓이는 바깥쪽 삼각형보다는 작고, 안쪽 삼각형보다는 크다. 다시 말해서, 바깥쪽 삼각형은 버려야 하는 부분을 가지고 있고, 안쪽 삼각형은 채워야 하는 부분을 가지고 있다. 게다가, 두 삼각형의 크기 비율은 4:1로 "이 사이에 원의 크기가 있어."라고 말하기에는 범위가 너무나도 크다. 그래서 아르키메데스는 삼각형이 원과 맞대고 있는 점들 사이에 점을 또 그려서 더 작게 만들었다.
다음 단계에서는 정육각형이고, 이것의 넓이도 잘 구할 수 있다. 두 정육각형의 크기 비율은 4:3으로 삼각형보다 차이가 더 줄어든 것을 확인할 수 있다. 다음 단계는 정12각형으로 크기 비율이 약 1.07:1로 많이 줄어든 것을 확인할 수 있다. 이 단계를 계속 거치면 그 차이가 현저하게 줄어든다.
아르키메데스는 이 방법을 통해 정96각형 즉, 이짓거리를 5번을 해서 223/17과 22/7 사이에 반지름이 1인 원의 넓이가 있다는 것을 알아냈다.[28] 적어도 무엇보다는 크고, 적어도 무엇보다는 작다는 것을 이용해서 어떤 값을 얻어내는 것이 적분의 핵심이다. 이런식으로 양쪽을 조여서 근사한 어떤 값을 얻어내는 방법을 조임정리 혹은 샌드위치 정리라고 한다.
적분법
[+/-]
위와 같이 아주 작게 잘라 붙여넣으면 자투리가 아주 작아져서 무시할 수 있을 정도로 작아진다. 알뜰살뜰하게 하나하나 다 모아서 쌓는 것이 바로 적분이다. 뉴턴은 적분을 미분과 같이 묶었지만, 사실 오늘날에는 엄밀한 것을 좋아하는 수학자들이 만든 적분법을 사용한다.
고대부터 사용했던 적분은 도형에 대해서 사용했다. 하지만 이제는 그래프를 그려서 적분을 사용한다. 리만 적분의 아이디어는 아르키메데스의 아이디어와 일치한다. 리만 적분에서도 조임정리가 사용된다. 아르키메데스의 생각보다 더 나아간 것은 복잡한 식을 통해서 얻는 방식 대신 너비와 높이만 곱하면 구해지는 직사각형을 사용한다는 점이다.[29]
리만적분
[+/-]
오른쪽 그림은 리만적분의 한가지 예시이다. 오른쪽 그림처럼 주어진 구간을 똑같이 나눠서, 한쪽은 원래 그래프의 넓이(가운데 그림)보다 작게(왼쪽 그림), 나머지 한쪽은 원래 그래프의 넓이보다 크게(오른쪽 그림) 만든다. 계속 구간을 잘게 나누면 결국엔 가운데 그래프의 넓이에 무한히 가까워질 것이다.
이 방법은 사실 컴퓨터 프로그래밍을 사용하면 쉽게 값을 얻을 수 있다. 코드를 위에서 말한 것 그대로 넣어서 만들면 수학자들이 고생하면서 얻은 공식들을 쓰지 않고도 쉽게 적분 값을 얻을 수 있다. 하지만 적분에는 유용한 공식들이 있고, 개념적으로도 알고 있으면 응용하기 편하니, 먼저 짚고 넘어가자.
오른쪽 그림에 나와있는 그래프를 을 나타내는 그래프라고 하자. 어차피 그래프에 문자가 표시되어 있지 않으니 그렇게 해도 큰 상관이 없다. 오른쪽 그림에서 초록색이 그래프의 밑넓이를 나타내고, t=0에서 t=2까지의 밑넓이를 구한 것으로 보인다. 파란색 막대들은 합쳐도 초록색보다 부족한 넓이를 가지고, 빨간색 막대들은 합치면 초록색보다 큰 넓이를 가진다. 아르키메데스의 원의 넓이를 구하는 방법에서 보았듯이, 파란색과 빨간색을 촘촘하게 만들면, 초록색에 가까워질 것 같다.
먼저 왼쪽 파란색 막대를 한 번 보자. 0부터 2까지의 구간을 7등분 한 것 같아보이는데, 막대의 높이는 막대의 왼쪽 좌표의 y값을 따라가서, 막대가 6개가 있는 것을 확인할 수 있다. 반면에 오른쪽 빨간색 막대는 막대의 오른쪽 좌표를 높이로 삼아서 7개가 있는 것을 확인할 수 있다. 이것들의 합을 표로 표현하면 다음과 같이 나온다.
| t | |||||||
| 막대높이 | 0 | ||||||
| 누적 막대 넓이 | 0 | 0.02332 | 0.11662 | 0.32653 | 0.69971 | 1.2828 | 2.12245 |
| t | |||||||
| 막대높이 | |||||||
| 누적 막대 넓이 | 0.02332 | 0.11662 | 0.32653 | 0.69971 | 1.2828 | 2.12245 | 3.26531 |
표에서 나와있듯이, 두 값의 차이는 크지만, 근본적으로 이 차이는 빨간색 막대 중 가장 마지막의 막대와 (여기서는 보이진 않지만) 파란색 막대 중 맨 첫번째 막대의 넓이 차이다. 아르키메데스의 방법처럼 좀 더 잘게 자르면 더 근사한 값이 나올 것이다.
| t | ||||||||||||||
| 막대높이 | 0 | |||||||||||||
| 누적 막대 넓이 | 0 | 0.00292 | 0.01458 | 0.04082 | 0.08746 | 0.16035 | 0.26531 | 0.40816 | 0.59475 | 0.8309 | 1.12245 | 1.47522 | 1.89504 | 2.38775 |
| t | ||||||||||||||
| 막대높이 | 4 | |||||||||||||
| 누적 막대 넓이 | 0.00292 | 0.01458 | 0.04082 | 0.08746 | 0.16035 | 0.26531 | 0.40816 | 0.59475 | 0.8309 | 1.12245 | 1.47522 | 1.89504 | 2.38775 | 2.95918 |
막대의 넓이합의 차가 더 줄어든 것을 확인할 수 있다. 맨 마지막의 빨간색 막대는 이런식으로 줄이다보면 1/2씩 작아질 것이다. 하지만, 맨 마지막의 막대의 넓이가 줄어들기만 하는 것이 아니다. 마지막 막대의 밑면의 길이가 줄어들수록, 다른 막대들이 들어갈 공간이 생기기 때문에, 파란색 막대의 넓이합을 보았을 때, 넓이합이 증가한 것을 볼 수 있다. 이와 같은 과정을 계속 반복하다보면 이 막대들의 넓이합은 초록색 영역의 넓이인 2.666666에 가까워질 것이다.
(코딩을 통해서 이러한 접근법으로 초록색의 넓이를 근사하게 구해볼 수 있다.)
적분공식
[+/-]적분을 구하는 방법은 있지만, 적분할 대상은 다양해서 아예 적분표(Integral table)가 따로 있다. 수많은 적분식들이 정리되어 있기 때문에, 특수한 경우가 아니면 적분표를 사용하는게 편하다. 이 중에서도 우리가 이 곳에서 다룰만한 것들은 아래 두 가지이다.
- (단, )
- 그리고
기호 는 적분기호로, 와 함께 쓰여 "라는 파라미터에 대해서 와 안에 있는 함수를 적분하겠습니다."라는 의미를 가지고 있다. 가 아니라 에 대해서 적분하고 싶으면 대신 를 적으면 된다.
기호는 꼴로 더 자주 쓰이는데, 이것은 "여기()부터 저기()까지 적분해 주세요."라는 뜻이다. 와 가 안 붙어있는 기호의 경우 어디서부터 어디까지 적분해야 하는지 모르기 때문에 적분상수 C를 붙인다. 시작점을 알 수 없으니 알아서 정해서 사용하라는 뜻이다.
알아서 정해서 사용하라는 뜻은 내가 알아서 정해서 사용하라는 뜻도 되지만, 남도 알아서 정해서 사용한다는 뜻도 가지고 있다. 그래서, 부정적분을 하면서 C는 어떤 값이라고 내가 말해도, 다른 사람이 다른 값으로 사용할 수 있기 때문에 대부분의 경우 정적분을 사용한다.
1번은 자주 사용하는 적분으로, 를 에 대해서 적분하면 가 되고, 를 에 대해서 적분하면 가 된다. 또, 는 이므로 를 에 대해 적분하면 이다.
또, n이 -1이 아닌 모든 경우에 성립한다. 정수가 아니어도 되고, 유리수가 아니어도 되고, 실수가 아니어도 되고, 심지어 복소수가 아니어도 된다.
2번의 경우 미분꼴로 나타냈을 때 더 눈에 쉽게 들어온다. 삼각함수 과 이 서로가 서로에게 엮여있는 관계라고만 알고 지나가도 괜찮다.
미분
[+/-]미분(微分)은 아주 작게(微) 나누어(分) 변화를 관찰하는 것이다. 영어로는 differential로 나타나는데, 영단어 자체는 차이를 강조하는 말이다. 미분은 derivative의 번역어이기도 한데, 영어로는 두 단어로 구분하지만, 한국어에서는 두 단어를 구분하지 않는다. 전자는 미분이라는 행동을 말하고, 후자는 미분해서 나온 결과(도함수)를 말한다고 한다.
미분은 적분에서 그랬던 것처럼, 아주 작게 잘라서 미세한 변화를 보는 것이다.
제논의 역설
[+/-]장화처럼 생긴 이탈리아 반도, 발등의 끄트머리에는 고대에 엘레아라고 불리던 지역이 있다. 그리고 그곳에서 제논이라는 사람이 사람들에게 이상한 역설을 만들어 설파했다. 어떤 것이든지 어떠한 결과로 이르는 것은 말이 안된다는 것이다.
고대 그리스의 영웅 아킬레우스는 먼저 가고 있는 거북이를 제칠 수 없다고 주장한다. 먼저가고 있는 거북이가 있는 지점까지 아킬레우스가 달리면, 그 시간동안 거북이는 앞으로 나갈 것이고, 아킬레우스가 또 달려서 그 거리를 따라 잡으면 거북이는 또 그 시간동안 앞으로 나간다고 주장한다.
미세한 변화
[+/-]
이 역설은 우리에게 시간이라는 개념을 상기시켜 준다. 당연히 아킬레우스는 거북이보다 빠르고, 당연히 어느 순간을 지나면 아킬레우스가 거북이를 제칠 것이다. 하지만 그 순간은 어디인가? 미리 그 순간을 선언하고 난 다음에 반대로 언제 출발했는지를 구해도 되겠지만, 그럼 언제 출발했는지는 알 수 있을까? 제논의 역설은 (단 한 사람만 빼고)논증을 좋아하는 고대 그리스 사람들에게 제대로 설명하지 못하는 역설을 만들어냈다.
영문 위키에 의하면[30] 이건 엡실론-델타 논법이라는 개념이 정립되고 나서야 논증이 되었다고 한다. 이 논법이 무슨 논법인지는 차치하고, 무한소에 대해서 알아보자.
역설에서 강조하고 있는 건 아무리 아킬레우스가 거북이를 쫓아가고 있더라도, 아주 작은 시간동안에서 보면, 아킬레우스는 거북이를 제칠 수 없다는 것이다. 이것을 더 시각적으로(혹은 수치적으로) 보기 위해, 아킬레우스의 달리기 속도와 거북이가 움직이는 속도, 아킬레우스가 거북이가 출발한 후 출발한 시간을 가정할 것이다.[31]
먼저 거북이의 속도를 라고 하자. 그리고, 아킬레우스의 속도를 라고 하자. 아킬레우스는 거북이가 출발한 지 9초가 지나서야 출발한다. 얼마로 잡든지 아킬레우스의 다리가 거북이보다 빠르기만 하면 제논의 역설에서 벗어나지 않는다. 하지만 저 숫자들이 왠지 모르게 마음에 드니 이렇게 상정하자.
거북이가 출발한지 9초 뒤, 아킬레우스는 0m에서 이제 출발을 하고, 거북이는 아킬레우스보다 9m 앞에 있다. 그리스의 위대한 영웅 아킬레우스는 거북이를 쫓아 9m를 갔다. 이 때는 거북이가 출발한 지 9.9초 뒤일 것이다. 그런데, 제논의 역설에 따라, 0.9초 동안 거북이가 0.9m를 나아갔다. 그러니까, 거북이는 출발선에서 9.9m를 나아간 것이다.
아킬레우스는 계속해서 거북이를 제치기 위해 0.9m를 움직였다. 아킬레우스는 0.9초에 9m를 움직이므로, 0.09초가 더 지난 이 순간은 거북이가 출발한 지 9.99초 뒤일 것이다. 그런데 마찬가지로, 거북이는 그 0.09초 동안 0.09m를 나아갔다. 출발선에서 9.99m 떨어진 위치이다.
아킬레우스는 또 쫓아가고, 9.999초에 9.99m에 닿았지만, 거북이는 그보다 0.009m 나아갔다. 그렇게 아킬레우스는 계속해서 거북이를 쫓아가고, 쫓아가서 어느샌가 이 이야기를 수십번, 수백번 반복할 무렵에 9.9999999999999...m를 움직였다. 물론 거북이는 그것보다 0.0000000000...0009m를 더 나아갔다. 아킬레우스는 이야기를 찢고 마침내 거북이를 제쳤다. 아킬레우스가 뛰기 시작하고 나서 어느 순간에 지나갔을까?
우리는 답을 알고 있지만, 아마 납득하기는 힘들 것이다. 아킬레우스는 0.9999999999...초로 반복되는 어느 순간에도 거북이와 같은 위치에 있었던 적이 없었지만 1초보다는 작은 어느 순간에 같은 위치에 있을 것이라 생각하지만, 아킬레우스가 거북이와 같은 위치에 있는 순간은 1초라고 말하고 있기 때문일 것이다. 그 오묘하면서 모를 것 같은 간격을 무한소라고 하자. 즉 이 되게 하는 를 상정을 하자.
이 내용은 수학적으로 엄밀성이 떨어지는 내용이다. 하지만 뉴턴도 이런 방식으로 미적분학을 썼으니, 잠깐 실례하고 무한소를 받아들이자.(엄밀하게 이런 것에 대해서 정의한 방법(엡실론-델타 논법)에 대해서는 미적분학을 참고하라.)
순간의 변화율
[+/-]미분은 간단하게 말해서 함수의 기울기이고, 조금만 더 자세하게 말하면 A에 대해서 b에 대한 순간 변화율이다.[32] 즉, b가 어떤 값을 갖냐에 따라 값이 달라지는 A에 대해서 아주 조그마한 b의 변화에 A가 얼마나 달라지는지를 보는 것이다. 대표적으로 주식차트를 생각해볼 수 있다. 주식은 시간에 따라 값이 달라지기 때문에, A는 1주의 가격, b는 시간으로 보면 된다.
A가 b에 따라 값이 바뀌는 것을 강조하기 위해 A를 달리 표현할 수 있다. 지금 b가 무슨 값인지 알아야지 A를 알 수 있으므로, 오일러 할아버지의 표기에 따라 다음과 같이 쓴다.
여기서 A라는 값의 표기는 바뀌지 않고, b의 값을 넣어서 A의 값을 나타낼 수 있다. 즉, b를 1이라고 하고, b가 1일 때 A가 56,000원이면
- \
처럼 표현하는 것이다.
하지만 위의 표기는 변화량을 말하는 것이 아니라, b가 특정한 값일 때의 A의 값이다. 우리가 변화량을 말하기 위해서는, 이런 특정한 값이 아니라, "아침에 주식을 봤는데 샀을 때보다 주당 5000원이 올랐어!" 같이 어떤 비교할 것이 존재하고, 그것에 대해 값이 얼마나 바뀌었는지를 말해야 한다. 또, 이렇게만 말하면 비교가 잘 안되기 때문에, "b값이 얼마나 바뀌는 동안"이라는 수식어도 있어야 한다. 단순하게 말해서 위의 문장하고 "10년 동안 묵혀놓은 주식이 샀을 때보다 주당 5000원이 올랐네."라는 문장을 받아들이는 느낌이 다르지 않은가.
첫번째 문장을 수식으로 표현하면 다음과 같이 표현될 것이다.
- \
미분은 이런 변화보다도 더 짧은 시간의 변화를 원한다. 커피 한 잔을 즐길 시간도 없이 치고 빠지는 것을 좋아하는 사람들에겐 저런 여유가 없다. 주식에서 빨간봉 파란봉은 하나의 변화를 담는 시간에 따라 월봉(月棒), 주봉(週棒), 일봉(日棒)이라고 부르는데, 단타에서는 일봉보다도 더 짧은 시간인 분봉(分棒)마저도 길게 느껴질 것이다. 분을 다투는 순간에서의 가격변화량은 다음과 같이 쓸 수 있을 것이고,
- (단, 여기서 는 변하기 전의 어떤 시간)
1초 사이의 시간마저 다투는 순간에서의 가격변화량은
- (s는 초 단위)
일 것이다. 이제 제논의 역설로 돌아가보자. 아킬레우스가 거북이를 제치는 순간, 그 순간과, 그 직전의 제논의 역설 속에 갇힌 아킬레우스가 거북이를 무한히 쫓아가는 순간의 차이 h를 꺼낼 때가 왔다. 1초 사이의 시간보다도 더 작은 순간의 가격변화량은 어떻게 표현할까? 아주 작은 단위의 h를 표현한다면 아마 쉽게 구할 수 있을 것이다. 그러면 아주 짧은 순간의 가격변화량은
로 표현된다. 이것이 주식 가격에 대한 시간의 순간변화량, 즉 미분이다.[33] 여기서는 h를 순간의 차이라고 말했지만, 보통의 경우 h는 그냥 문자에 불과하기 때문에 격식을 차린 표현으로 다음과 같이 쓴다.(물론 미적분학이 처음 나왔을 때는 쓰지 않은 표현이었다.)
는 limit의 약자로 극한이라고 불린다. 의 의미는 h를 0으로 보낸다는 뜻으로, h가 0은 아니지만 아주 0에 가까운 어떤 수여서 0하고 구분하기가 힘들다라고 하는 뜻을 지니며, 제논의 역설의 그것과 맥락상으로는 똑같다고 봐도 큰 무리는 없다.(물론 정확하게 알기 위해서는 엡실론-델타 논법을 봐야 한다.) 이왕 점잖게 하는 김에 더 점잖게 표현하는 것이 하나 더 있다. 어떤 A에 대해서 b의 미분을 적을 때, 위 식처럼 길게 늘어 쓰는 것이 아니라 두 가지 표현법이 있다. 하나는 다음과 같이 나타내는 것이고,
하나는 다음과 같이 나타내는 것이다.
위쪽의 식은 라이프니츠 표기법으로, 미분의 대상은 위로, 그 대상을 미분시킬 물리량은 아래로 보내서 적는다. 고트프리트 빌헬름 라이프니츠가 고안한 표기법으로, 미적분학의 태동기에서 미적분을 만든 인물이다. 변화시킬 것과 변화 시키는 재료를 둘 다 표현했기 때문에 모호함이 없게 멋들어진 표기법이다.
아래쪽의 식은 뉴턴 표기법으로, 미분의 대상 위에 점만 찍어서 미분을 표현하는 표기법이다. 아이작 뉴턴이 고안한 표기법으로, 라이프니츠와 마찬가지로 미적분을 만든 인물이고,[34] 위에서 보았듯, 물리학의 역사에서 아주 큰 영향력을 미친 인물이다. 그런 영향력과는 달리 표기법이 심플한데, 이 표기법은 오로지 시간에 대한 미분을 고려해서 만들었기 때문에 그런 것이다. 여백의 맛이 돋보이는 표기법이다.
두 표기법 중에서 더 자주 쓰는 것은 라이프니츠 표기법이다. 뉴턴의 표기법은 너무 생략되어서, 범용성이 너무 낮기 때문이다. 심지어 뉴턴의 표기법은 라이프니츠 표기법으로
로 쓸 수 있기 때문에, 가끔씩 라이프니츠 표기법으로 쓰기도 귀찮을 때 뉴턴 표기법이 쓰인다.
예시
[+/-]간단하게 미분의 예제를 하나 생각해보자. 우리는 이 문제를 풀 때 격식있게 를 사용할 것이다. 간단하게, 와 에 대한 미분을 구해 볼 것이다. 는 다음과 같이 주어진 함수다.
위의 식에 비추어보아 임의의 시간 에 대해서 의 미분은 다음과 같을 것이다.
우리가 중학교 때 배운 곱셈공식에 따라서 위 식은
이 된다. 그런데 는 h보다 더 작으므로 무시할 수 있다.[35] 따라서 약분하면
이다. 라이프니츠 표기법은 좀 더 직관적인 것이, 표기법에서 나오는 d는 차이를 나타내는 단어에서 유래한다. 즉, dy는 y의 순간적인 변화, dt는 t의 순간적인 변화를 말하는 것이다. 그래서 두 순간적인 변화의 비율을 따지기 때문에 순간 변화율, 즉 미분을 표기한 것이다.
이것도 컴퓨터 코딩을 이용해서 수치적으로 구해볼 수 있을 것이다.
미분 공식
[+/-]미분 역시 적분처럼 자주 쓰이는 형태들이 존재한다. 다만, 적분공식을 구하는 것에 비해 비교적 쉽기 때문에 적분과는 달리 표까지 정리해 놓지는 않는다. 자주 사용되는 미분식들은 다음과 같다. 미분을 표기하는데 있어서 미분하는 물리량은 식에 나와있으므로, 단순히 함수 뒤에 '를 써서 표기하였다.
- (C는 상수)[36]
- (단, 인 모든 실수)
 |
이 글은 편집중입니다. 누가 언제 마지막으로 글을 썼으며 그리고 쓰고 있는지는 문서역사에서 살펴 보시기 바랍니다. |
운동의 예시
[+/-]위에서 운동의 요소와 법칙을 다뤄봤다면, 여기서는 그 운동의 대표적인 예시들을 다룰 것이다. 예시라고는 했지만, 실용적이기보단 이론적인 것들을 중심으로 보여줄 것이고, 후에 다룰 것들에도 적용할 수 있는 운동을 중심으로 선정하였다.
등속 운동
[+/-]가속도가 하나도 없는 운동이다. 힘이 없는 운동이다. 정확히는, 우리 우주 안에 있는 모든 것들은 중력이라고 하는 힘을 받기 때문에[37] 중력을 상쇄하는 힘도 받아서 물체가 받는 힘의 총 합이 0인 물체가 움직이는, 혹은 멈춰있는 운동이다.
힘은 벡터다. 그리고 같은 차원의 벡터끼리는 합 연산이 가능하다. 단순하게 같은 벡터인 속도를 예를 들 수 있다. 시속 100km로 달리는 트럭에서 거꾸로 시속 100km의 속도로 야구공을 던지면, 트럭은 앞으로 시속 100km로 가고, 야구공은 뒤로 시속 100km로 던졌으므로, 두 개의 합은 시속 0km이므로, 야구공을 던진 순간을 촬영하면 야구공이 앞으로도, 뒤로도 움직이지 않는다.[38]
마찬가지로, 힘 역시도 합 연산이 가능해서 작용하는 힘에 반대방향으로 같은 크기의 힘을 주면 힘의 합은 0이다. 실질적으로 물체에 작용하는 힘은 개별적인 힘이 아니라 모든 힘의 합이고, 이를 알짜힘이라고 부른다.
등속 운동은 힘을 받지 않으므로, 가속도는 0이고, 관성의 법칙에 따라 계속 한 방향으로 같은 속력을 지닌 채 움직인다. 시간이 지날 때마다 물체의 위치는 같은 간격으로 변한다.
얼음 위에서 미끄러지는 물체는 사실 감속 하긴 하지만, 등속 운동에 가깝다. 또, 우리가 서 있는 것 역시 등속 운동이다. 지구의 중력으로 인해 우리는 지구와 우리의 질량중심으로 끌려가지만, 우리의 무게만큼 바닥이 우리를 밀어내고 있기 때문에(작용-반작용 법칙) 우리가 서 있을 때 속력이 0인 등속운동을 한다. 바닥이 바닥면의 수직방향으로 힘을 주기 때문에 수직항력이라고 부른다.
수직으로 힘을 준다고 말할 수 있는 것은 경사진 빙판길 생각하면 알 수 있다. 빙판길은 미끄럽고, 경사진 빙판길에 서 있으면, 우리는 아래로 미끄러질 것이다. 경사진 빙판길에 서 있는 순간을 생각해보면, 고려할 힘은 중력과 수직항력 밖에 없는데, 만약에 수직항력이 항상 중력과 반대 방향으로 작용한다면 미끄러질 이유가 없다.
등가속 운동
[+/-]
가속도가 똑같은 운동이다. 힘이 일정하게 주어진 운동이다. 가속도가 0일 때는 등속 운동과 같다. 가속도가 0이 아닐 때는 속력을 시간이 지날 때마다 같은 간격으로 바꾼다. 그리고 위치는 속력이 올라가는 만큼 바뀐다.
이상적이진 않지만, 표로 그려서 생각해볼 수 있다.
속도는 위치의 변화를 시간으로 나눈 값이므로, 반대로 속도와 시간을 곱하면 위치의 변화가 나온다. 시간이 지날 때마다 바뀐 속도에 맞춰 위치의 변화를 더해주면 위치를 구할 수 있을 것이다.
속도가 0인 물체가 1m/s^2의 가속도로 움직일 때 속력과 위치를 표현하면 다음과 같이 나타난다.
| 시간 | 0초 | 1초 | 2초 | 3초 | 4초 | 5초 | 6초 | 7초 | 8초 |
| 속도 | 0m/s | 1m/s | 2m/s | 3m/s | 4m/s | 5m/s | 6m/s | 7m/s | 8m/s |
| 위치 | 0m | 1m | (1+2)m=3m | (1+2+3)m=6m | 10m | 15m | 21m | 28m | 36m |
사실, 위 값은 제대로 된 값이 아니다. 시간을 좀 더 촘촘하게 나눠서 계산하면 또 다르게 나온다.
| 시간 | 0초 | 0.5초 | 1초 | 1.5초 | 2초 | 2.5초 | 3초 | 3.5초 | 4초 | 4.5초 | 5초 | 5.5초 | 6초 | 6.5초 | 7초 | 7.5초 | 8초 |
| 속도 | 0m/s | 0.5m/s | 1m/s | 1.5m/s | 2m/s | 2.5m/s | 3m/s | 3.5m/s | 4m/s | 4.5m/s | 5m/s | 5.5m/s | 6m/s | 6.5m/s | 7m/s | 7.5m/s | 8m/s |
| 위치 | 0m | 0.25m | 0.75m | 1.5m | 2.5m | 3.75m | 5.25m | 7m | 9m | 11.25m | 13.75m | 16.5m | 19.5m | 22.75m | 26.25m | 30m | 34m |
이 값도 사실 제대로 된 값이 아니다. 또다시 반으로 잘라서 4초까지만 적어보면 또 다르게 나온다.
| 시간 | 0초 | 0.25초 | 0.5초 | 0.75초 | 1초 | 1.25초 | 1.5초 | 1.75초 | 2초 | 2.25초 | 2.5초 | 2.75초 | 3초 | 3.25초 | 3.5초 | 3.75초 | 4초 |
| 속도 | 0m/s | 0.25m/s | 0.5m/s | 0.75m/s | 1m/s | 1.25m/s | 1.5m/s | 1.75m/s | 2m/s | 2.25m/s | 2.5m/s | 2.75m/s | 3m/s | 3.25m/s | 3.5m/s | 3.75m/s | 4m/s |
| 위치 | 0m | 0.0625m | 0.1875m | 0.375m | 0.625m | 0.9375m | 1.3125m | 1.75m | 2.25m | 2.8125m | 3.4375m | 4.125m | 4.875m | 5.6875m | 6.5625m | 7.5m | 8.5m |
이 과정을 반복하진 않지만, 시간을 아주 작게 잘라서 다시 맞추면 위치표는 다음과 같이 나온다.
| 시간 | 0초 | 1초 | 2초 | 3초 | 4초 | 5초 | 6초 | 7초 | 8초 |
| 속도 | 0m/s | 1m/s | 2m/s | 3m/s | 4m/s | 5m/s | 6m/s | 7m/s | 8m/s |
| 위치 | 0m | 0.5m | 2m | 4.5m | 8m | 12.5m | 18m | 24.5m | 32m |
위치를 보면 위치가 시간에 따라 일정하게 증가하지 않음을 볼 수 있다. 위치는 시간에 따라 곱절로 증가한다. 더 쉽게 보기 위해서 위치에 2를 곱하면
| 시간 | 0초 | 1초 | 2초 | 3초 | 4초 | 5초 | 6초 | 7초 | 8초 |
| 위치 | 0m | 1m | 4m | 9m | 16m | 25m | 36m | 49m | 64m |
시간에 제곱으로 증가하는 것을 볼 수 있다. 즉, 물체가 속도가 0일 때 등가속 운동을 하면 물체의 위치는 시간의 제곱으로 증가한다.
우리가 물리량을 정의할 때 시간의 변화로 정의했는데, 시간은 초 단위로 바뀌는 것이 아니다. 0초와 1초 사이에는 0.5초가 있고, 0초와 0.5초 사이에는 0.25초가 있다. 또, 0초와 0.25초 사이에는 0.125초가 있고, 0초와 0.125초 사이에는 0.0625초가 있다. 시간을 계속 쪼개고 쪼개더라도, 고전역학에서 시간은 언제나 그것보다 작은 값이 존재한다.[39]
위의 과정은 자를 사용해서 위치를 재는 것으로 비유할 수 있다. 첫번째의 경우, 위치를 알기 위해서 초 단위를 자로 사용하는 것이고, 두번째는 반 초 단위를 자로 사용하는 것이다. 세번째는 반의 반 초 단위를 자로 사용하는 것으로, 더 세밀한 자를 사용하면 사용할수록 정확한 값을 얻을 수 있다. 이렇게 크기를 재는 행위를 적분이라고 부른다.[40] 적분에는 여러가지 방법이 있는데, 물리학에서는 미분이라는 도구와 함께 미적분학을 사용한다.
물리학에서 (시간 혹은 공간에 대한)순간의 물리량의 변화는 미분으로 표현이 되고, (시간 혹은 공간에 대한)물리량의 변화의 합은 적분으로 표현된다.
등가속 운동에서 위치는
위치=속도*시간+가속도*(시간^2)/2+(초기 위치)
로 나타난다.
정리하면, 등가속 운동은 속도가 일정하게 증가하고, 위치는 시간의 제곱으로 변한다.
포물선 운동(ballistic motion)
[+/-]

포물선 운동은 두 가지로 나뉜다. 하나는 일정한 힘이 물체가 움직이는 모든 공간에서 적용된 체로 발사된 탄도 운동(ballistic motion)이고, 다른 하나는 물체가 무한대에서 입사각이 0도나 180도가 아닌 방향으로 들어와, 아주 거대한 중력이나 전기력을 가진 점입자에 의해 나타나는 궤도 운동(trajectory motion)이다. 후자의 경우는 궤도 운동의 종류를 다룰 때 더 자세하게 다룰 것이다. 여기서 말하는 것은 전자이다.
포물선 운동은 아래 방향으로 일정한 힘이 작용하고 물체가 다른 힘을 받지 않을 때 나타나는 운동이다. 다시 말해, 등가속운동의 특수한 경우이다.
등가속운동에서 물체의 위치는 가속도와 시간의 제곱을 곱한 값을 2로 나눈 값으로 나타난다고 했었다. 앞으로 움직이는 물체가 뒤로 가속도를 받으면 속력이 줄어들면서 점점 감속하는 운동을 한다. 속력이 0이 되어도, 계속 가속도를 받고 있으면 속도는 더 감소하기 때문에, 멈춘 물체가 뒤로 가속하는 운동으로 볼 수 있다.
이를 달리 해석하면, 속력이 0이 되는 순간을 전후로, 물체는 시간적으로 대칭적인 운동을 한다고 볼 수 있다. 즉, 속력 0을 기준으로 시간을 0초로 잡고, 앞 뒤 시간을 비교했을 때, 시간이 0에서 음수로 줄어들었을 때 뒤로 간 시간만큼 시간의 제곱으로 위치가 변하고, 시간이 0에서 양수로 늘어났을 때도 앞으로 간 시간만큼 시간의 제곱으로 위치가 변하는 것이다.[41]
이제 물체가 힘의 방향에 대해 비스듬한 방향으로 어느 한 속력을 갖고, 발사되었다고 하자. 물체에 작용하는 힘은 아래 방향으로 작용하므로, 고개를 돌려, 위를 앞으로 해석하면, 물체는 앞으로 진행하면서 뒤로 일정한 힘을 받는 운동으로 볼 수 있다. 동시에 이상하게 떨어지는 혹은 올라가는 운동을 한다.
고전역학에서 다루는 공간에서는 벡터를 직각으로 나눠서 생각할 수 있다.[42] 위 상황에서 직각으로 나뉜 두 벡터는 별개의 것으로 생각할 수 있다. 다시 말해서, 비스듬하게 발사된 물체의 운동을 힘이 작용하는 방향에 대한 운동 하나와, 힘이 작용하는 방향에 수직인 운동 하나로 쪼개서 생각할 수 있다.(이것은 이 운동에서 속력에 의존하는 공기저항이 없다고 가정해서 가능한 일이다. 속력에 의존하면 두 운동은 서로 연관성이 있어 위와 같은 해석이 불가능하다.)
그래서 물체는 힘이 작용하는 방향으로는 등가속운동을, 그 수직된 방향으로는 등속운동을 한다. 직교좌표 위에 한 축을 등가속운동에서, 다른 축을 등속운동에서 물체의 위치로 생각하고 물체의 두 운동의 좌표를 그려보면 포물선을 얻을 수 있다.
포물선이 나오는 이유는 위키백과의 포물선 문서에서 잘 나와있다. 이차곡선인 원과 타원과 쌍곡선도 직교좌표에서 제곱을 통해서 표현할 수 있다.
등속원운동
[+/-]
원은 고대세계와 중세, 르네상스에서도 완전한 것이었다. 물리학에서도 원운동은 여전히 중요한 운동이고, 지구의 공전궤도 역시 원운동에 가까운 타원운동을 한다.
등속원운동은 속도가 매 순간 바뀌는 운동이다. 속력은 같지만, 그 방향이 달라지는 운동이다. 즉, 매 순간 힘을 받는 등속력 운동이다. 비록 방향이 달라지지만 그 양은 같다는 것은 작용하는 힘의 크기 역시도 일정하다는 것을 시사한다. 또 매 순간 등속력으로, 원으로 운동한다는 것은 매 순간마다 바뀌는 방향의 각도 역시도 같다는 것을 시사한다. 또, 그 방향은 물체의 뒤에서 봤을 때 한쪽으로 들어가 있고(그림에서는 왼쪽), 매 순간 뒤에서 봤을 때 똑같기 때문에, 힘이 작용하는 방향은 원 안의 어느 점이라는 것을 알 수 있다. 등가속운동에서 사용했던 방법을 사용하면, 점점 그 힘은 원의 중심에 가까워지는 것을 볼 수 있다.
즉, 등속원운동은 원의 중심 방향으로 일정한 힘을 가지고 물체를 잡아당기는 운동임을 알 수 있다. 그리고, 이 힘의 크기에 따라 가지는 원의 크기는 달라진다. 실에 달아놓은 공을 돌릴 때는 힘의 크기와 원의 크기는 상관 없을 것이라고 생각할 수 있는데, 힘의 크기에 따른 원의 크기보다 실제 원의 크기에 따른 힘의 크기만큼을 실의 장력이 상쇄하고 있어서 그런 것이다.
현실에서는 쥐불놀이나, 슬링, 공군의 가속도내성강화훈련용장비, 입자충돌기, 원형 방사광 가속 등 다양한 역사와 다양한 배경에서 사용되고 있다.
(주기적인)진동
[+/-]
진동이라고 하면 보통 무작위로 떨리는 것을 생각할 수 있다. 그것은 fluctuation이라고 부른다. 또 다른 진동으로는 주기성을 지니는 진동이 있다. 목소리나 어떤 음을 내는 것은 일정한 주기를 가지고 떨리는데, 이런 소리들은 공기가 전달하는 에너지를 측정해서 파형으로 그릴 수 있다.[43] 이것을 물리학에서 Oscillation이라고 부른다.
물리학에서 Oscillation은 르네상스 시대에서의 원만큼 세상을 구성하는 중요한 요소 중 하나로 여긴다. 물리의 모든 것을 이 진동으로 설명하려고 하는 물리학도 있다.
물리학자들은 (복잡한 계산을 싫어해서)단순함을 추구하기 때문에 Oscillation 중에서 특히나 단순조화진동(Simple Harmonic Oscillation, SHO로 줄여서 부름)에 집중한다. 진동 중에서도 가장 단순한 형태의 진동으로, 두 점 사이를 계속 왔다갔다하는 진동이다. 등속원운동을 위에서 보는 것이 아니라, 옆에서 볼 경우 나타나는 형태이다.
단순조화진동은 삼각함수를 통해 표현이 된다. 사실 삼각함수라는 표현도 빗변을 1로 두었을 때 원에 대한 함수로 바뀌기 때문에, 삼각함수보다 원함수(圓函數)라는 표현이 더 받아들이기 쉽다.[44] 삼각함수의 sine은 위 그림에서 점이 (1,0)(가로축이 첫번째 좌표, 세로축이 두번째 좌표일 때)에서 반시계방향으로 증가할 때 점의 세로축 값이고, cosine은 점의 가로축 값이다. 다른 삼각함수는 위키백과의 삼각함수 문서를 참고하면 된다.

단순조화진동은 진동의 중심에서 삼각함수 중 sine과 cosine으로 표현이 된다. sine그래프를 옆으로 옮긴 것이 cosine이기 때문에 sine과 cosine을 딱 잘라 구분지을 필요는 없다. sine과 cosine의 중요한 특징은 변화 값에 있다.
위에서 언급했던 미분에 대해서 다시 한 번 집고 갈 필요가 있다. 미분은 속도나 가속도의 정의처럼, 어느 변화량을 관심 있는 값에 변화로 나눈 값을 의미한다. 더 정확히는 관심 있는 값에 따라 변하는 변화량에 대해서, 관심 있는 값이 아주 조금 바뀐 것에 따라서 변한 정도를 나타낸 값이다. 그 아주 조금은 등가속 운동에서 뛰어넘었던 과정 속의 시간 정도이고, 수학적으로는 극한이라는 개념을 도입해서 설명한다. 미분 자체는 운동 문단의 변화량에서 설명했듯이 시간이건, 공간이건, 에너지가 됐건, 깊이가 됐건에 상관없이 그것의 변화량을 나타내는 개념이다. 그래서 일정하게 상승하면 일정한 양수를, 급하게 상승하면 그만큼의 변화량을 반영한다.
sine과 cosine 둘 모두는 두 번 미분하면 부호가 바뀐 sine, cosine 값이 나온다. 다시 말해, 진동의 중심을 기준으로 진동은 위치와 물체가 받는 힘은 항상 반대다.
또, 한 번 미분 할 때는 값이 최대 혹은 최소일 때 미분 값은 0, 값이 0일 때는 미분 값이 최대 혹은 최소라는 특징을 갖는다. 즉, 속도가 0일 때는 (위치, 힘)이 (최대, 최소) 혹은 (최소, 최대)이고, 속도가 최대 혹은 최소일 때는 위치와 힘이 0이다. 또 sine을 미분하면 cosine이다.
한 번 sine의 미분 값을 살펴보자. 먼저, sine은 함수로 쓰일 때 로 사용하고, 시간()에 대해서 미분한다고 하자. 또, 시간에 대한 sine 함수는 로 나타난다고 하자.[45]
| 미분 횟수 | 0회 | 1회 | 2회 | 3회 | 4회 |
| 함수 |
4번 미분한 후에 다시 돌아온 것을 볼 수 있다. 또, , , 의 미분도 어떻게 될 것인지 볼 수 있다. 진동은 이런 미분에서의 순환성과 함께, 시공간의 순환성도 가지고 있기 때문에 에너지를 전달하는데 있어서 좋은 형태이다. 그래서 파동은 (전달하면서 손실되거나 에너지 밀도가 줄어드는 경우도 있지만)이런 꼴을 가지고서 퍼져나간다.
따라서 소리(음파), 빛(광파), 라디오(라디오파), 파도(물결파) 같은 현상들은 진동으로 표현을 한다.
에너지와 힘
[+/-]뉴턴역학은 주로 물체를 중심으로 물리를 기술하였고, 라그랑주역학은 주로 움직이는 장을 중심으로 물리를 기술하였다. 이 두 개의 물리량은 동떨어져있는 물리량이 아니다. 오히려 매우 밀접한 연관을 가지고 있는 물리량이다. 위에서 에너지는 일을 할 수 있는 능력으로 정의했다. 그리고 일은 특정 거리 동안 주어진 힘이다. 일은 동일한 힘이 지속적으로 주어졌을 때 다음과 같이 표현된다.
일 = 힘×(이동한 거리)
에너지는 이 일을 할 수 있는 능력이고, 단위도 일과 똑같다. 다시 말해, 에너지와 일은 비교가 될 수 있는 물리량이다. 위치에너지가 일정하지 않는 곳에서 물체가 움직일 때를 생각해보자. 물체(공)가 위치에너지가 기울어져 있는 곳(경사)에 위치하면 물체는 낮은 위치에너지를 찾아간다. 이 때에 물체는 움직이므로, 속력이 생겼고, 속력이 생겼다는 것은 가속도를 가졌다는 것을 의미한다. 가속도를 가졌다는 것은 힘이 작용했다는 것이고, 위의 일과 힘과 거리의 관계와 비슷하게, 힘은 다음과 같이 기술할 수 있다.
힘 = (에너지의 변화)/(이동한 거리)
즉 에너지의 거리에 대한 변화는 힘을 만들어낸다. 운동 에너지도 마찬가지다. 운동 에너지의 거리에 대한 변화는 힘을 만들어낸다. 또, 운동 에너지는 멈춰있는 물체가 일을 받아 움직였을 때 만들어지는 것이기도 하다. 운동 에너지는 위치에 의존하는 위치 에너지와 달리 움직임에 의존하는 에너지이기 때문에 운동 에너지는 다음과 같이 나타난다.
운동 에너지 ∝ 질량×(속력^2)
∝는 비례기호다. 고전역학이 발전했던 초창기에는 운동 에너지 값은 그냥 질량×(속력^2)로 보는 경우도 있었다.[46] 하지만 고전역학이 발전하면서 운동 에너지는 질량×(속력^2)/2 즉, 활력을 2로 나눈 값이라는 것을 알게 되었다. 그런데, 위에서 운동량을 정의했을 때, 운동량은 속도와 질량을 곱한 것이라고 정의했다고 말했었다. 즉, 운동 에너지를 다시 쓰면
운동 에너지 = (운동량^2)/(2×질량)
이다.
힘은 에너지의 변화를 거리로 나눈 것으로 표현했었다. 그런데 당구공 같은 걸 생각했을 때, 당구공을 당구공으로 쳤을 때, 에너지 전달이 일어난 거리는 매우 작다고 생각할 수 있다. 그럼 작은 값으로 에너지를 나눈 것이므로 당구공이 서로 주고받는 힘은 매우 커야 한다고 생각할 수 있는데, 그 말이 맞다. 하지만, 에너지가 전달이 되는 거리가 무한정으로 작은 것은 아니기 때문에 힘이 무한정 커진 것은 아니다.
당구공이 아주 단단한 물체가 아니기 때문에, 살짝의 연성을 가진다. 따라서 당구공이 부딪혔을 때, 순간적으로 당구공은 조금 찌그러지다가 다시 원래의 형태를 회복한다.[47] 즉, 에너지가 전달되는 거리가 있다. 에너지가 전달되는 거리가 있다는 것은 에너지가 전달되는 사건과 사건들이 존재한다는 것이기 때문에, 전달되는데 걸리는 시간이 존재한다. 따라서 힘은 무한정 커지는 것이 아니다. 또, 걸리는 시간이 존재하기 때문에, 힘이 커지는데 순간적으로만 커지는 것이 아닐 것이고, 에너지가 교환되고 나서 두 당구공은 운동에너지를 주고 받지 않으므로, 힘은 서서히 커지다가 최대로 커지면 다시 줄어들 것이다. 여기서 당구공이 주고받는 힘을 충격력이라고 부르고, 에너지를 교환하는 시간 동안 받은 힘을 전부 시간에 대해 더한 것을 충격량이라고 부른다.
충격력은 에너지를 주고받는 시간(충돌시간)이 길수록 높은 값을 가지지 못한다. 충격량 자체가 줄어드는 것은 아니지만, 충돌시간이 길어지면 물체가 받는 힘이 줄어들기 때문에 에어백이나 추락방지망 등의 안전장치들은 충돌시간을 늘리는 방식으로 작동한다. 캐치볼에서 공을 잡으면서 잡는 손의 팔을 뒤로 살짝 빼는 것도 같은 원리를 이용한 것이다.
중력
[+/-]뉴턴 경의 프린키피아에서 3가지 법칙이 뉴턴역학의 기본적인 원리가 되었다. 사실 프린키피아가 유명한 것은 그 기본적인 원리를 확립한 것 때문만은 아니다. 뉴턴은 프린키피아를 통해, 기존의 관측결과에 잘 들어맞는 만유인력의 법칙의 과정을 유도했다.
뉴턴 이전의 천문학에서 다양한 일들이 있었다. 프톨레마이오스가 천동설을 말하고, 아리스토텔레스가 정립하고, 코페르니쿠스가 지구가 태양 주위를 도는 것이 더 편하고 합당하다고 책으로 적고, 갈릴레이가 이에 동조했다. 튀코 브라헤가 자신의 모형을 어거지로 만들면서 반박하는 동안 튀코의 아주 좋은 눈으로 관측한 데이터를 가지고 케플러가 3가지 법칙을 발견하면서 뉴턴의 차례가 되었다.
위의 자질구레한 내용들은 앞으로 우리가 이야기할 내용들과 함께 맨 아래의 과학사 파트에서 정리하였다. 우리가 눈 여겨볼 것들은 케플러의 3법칙과, 뉴턴의 만유인력 법칙이다.
케플러는 튀코 브라헤라고 하는 당시 아주 저명했던, 그리고 오줌을 참는 것은 아주 위험한 행위임을 알려준 천문학자의 조수였다. 튀코 브라헤가 연회에서 오줌을 참다가 방광이 터져 죽은 후로 튀코가 생전 모았던 관측자료들을 통해 3가지 법칙을 주장한 것으로 유명한 인물이다. 케플러가 주장한 3가지 법칙은 다음과 같다.
- 행성은 태양을 한 초점으로 하는 타원 형태로 돈다. (타원궤도법칙)
- 행성과 태양에 가상의 선을 그었을 때, 행성이 어디있든지 상관없이, 행성이 이동한 시간이 같으면 그 선이 쓸고 지나간 면적은 같다.(면적속도일정법칙)
- 행성의 공전주기의 제곱은, 긴 반지름을 세 제곱에 비례한다.(행성조화법칙)
케플러의 이 법칙들은 튀코의 데이터를 바탕으로 하기 때문에 귀납적으로 굉장히 타당한 법칙들이었다. 다시 말해서, 튀코는 끝까지 지구는 돌지 않는다고 말했지만, 튀코가 가지고 있던 매서운 눈만큼은 그 누구에게도 지지 않을만큼 정확했다. 케플러는 이 세가지 법칙을 발표했지만, 왜 이런 법칙들이 성립하는지에 대한 답은 제시하지 못했다.
뉴턴이 이 법칙에 대해서 더 단순한 법칙들로 설명해나갔다. 기하학적으로 접근했는데, 이에 대해서는 《뉴턴의 프린키피아》(2015, 안상현 저)에서 자세하게 나와있다. 중·고등학생 수준에서의 기하학적 설명을 하기 때문에, 쉽게 읽을 수 있다.
제곱 반비례 법칙
[+/-]뉴턴이 제시한 법칙은 위에서 다루었던 세 가지 법칙과 만유인력의 법칙이다. 만유인력의 법칙은 질량을 가진 모든 물체가 질량을 가진 다른 모든 물체를 끌어당긴다는 법칙이다. 이 법칙은 거리에 대해 제곱 반비례 꼴로 나타나는 중력으로 설명할 수 있다.
중력 = 중력상수 × 물체 1의 질량 × 물체 2의 질량 / ((두 물체의 거리)^2)
즉 중력은 두 물체의 거리에 제곱에 반비례하여 줄어든다. 이것을 제곱 반비례 법칙 혹은 역제곱의 법칙이라고 부른다. 뉴턴 역학에 따르면, 굳이 물체와 물체가 붙어있지 않아도, 중력은 성립한다. 또, 그 거리가 제한되어 있지도 않다. 즉, 안드로메다에 있는 어떤 별과 지구에 존재하는 우리는 서로 끌어당기고 있는 것이다.
원격작용
[+/-]이를 원격작용이라고 한다. 원격작용은 쉽사리 받아들이기 어려운 초자연적인, 마술적인 주장이기 때문에 과학에서 받아들이기 어려운 현상이다. 이성적인 생각을 통해 쌓아올리는 과학을 마치 염동력을 부리는 것처럼, 윙가르디움 레비오사로 물체를 옮기는 것처럼 두 물체가 작용하는데 서로가 만나지도 않고 작용한다는 것은 매우 비과학적인 주장이 아닐 수 없었다.
뉴턴은 이 문제에 대해 옛날부터 존재한 개념인 에테르를 부정하지 않았다. 빛이 나아가기 위해선 빛이 나아가기 위해 거쳐야 하는 물질이 필요하다고 생각했고, 그것을 에테르라고 불렀다. 중력을 매개하는 물질이 무엇인지는 정하지 않았지만, 중력이 작용 가능하려면 물질이 반드시 필요하다고 생각했다.[48] 현대 물리학에서는 빛이 나아가기 위해선 물질이 필요하지 않다고 생각하고, 에테르 역시 존재하지 않는다고 받아들인다. 이것은 마이컬슨-몰리 실험에서 다시 다룰 것이다.
궤도
[+/-]
물체가 움직이는 길을 궤적이라고 한다.[49] 특히 천문학에서 물체가 일정한 패턴으로 움직이는 길을 궤도라고 한다.[50] 뉴턴은 만유인력의 법칙을 통해 행성이 가질 수 있는 네 가지 궤도를 제시했다. 그리고 이것은 모두 원뿔도형이다.
- 원 궤도
- 타원 궤도
- 포물선 궤도
- 쌍곡선 궤도

원과 타원, 포물선과 쌍곡선끼리는 비슷해 보이지만, 원과 포물선은 서로 비슷해 보이지 않는다. 하지만 이심률이라는 개념을 도입하면 네 원뿔도형을 하나로 합칠 수 있다.
이심률은 얼마나 원과 다른지를 나타내는 수치다.
원은 이심률을 0을 갖고, 이심률이 점점 증가하면 할수록 원과는 다른 도형이 된다.
이심률이 0에서 1 사이에 있으면 타원이라고 한다. 이심률이 1보다 작으면 도형은 양 끝이 서로 이어져 있다.
이심률이 1이면 포물선이 된다. 포물선을 보면 양쪽 끝이 서로 이어져 있지 않는 걸 볼 수 있다.
이심률이 1보다 크면 쌍곡선이 된다. 쌍곡선은 한 점을 중심으로 대칭적인 곡선을 가진다.
모든 원뿔도형은 초점을 가지고 있고(애니메이션에서의 붉은 점), 중력은 초점을 향해 작용한다.
원 궤도
[+/-]움직이는 물체에 비해 아주 커서 물체에 중력적으로 큰 영향을 주는 물체를 중력체라고 하자. 원 궤도의 경우 원의 초점이 중력을 주는 중력체의 중심이 있기 때문에 물체가 받는 중력의 방향은 항상 진행방향의 수직방향이다. 물체가 움직이는 속도가 정확히 중력에 맞아야 하는 운동이기 때문에 자연에서는 찾아보기 매우 힘든, 이상적인 궤도이다. 인공위성의 궤도 중에서 날씨 위성이나 지역의 통신 위성이 사용하는 정지궤도가 이 궤도를 따른다.
타원 궤도
[+/-]타원 궤도는 초점을 두 개를 가지고 있다. 하지만, 타원 궤도에서 중력의 영향을 주는 것은 한 초점에 존재하는 중력체이다. 타원궤도는 원 궤도와 달리 중력체와 물체와의 거리가 일정하지 않다. 어느 때는 멀어지고, 어느 때는 가까워진다. 타원궤도는 중력체와 가까워 질 때 즉, 중력이 증가할 때 속력이 커지고, 중력체와 멀어질 때 속력이 줄어든다. 중력체와 가장 가까울 때는 속력이 최대가 되고, 이 때 속도의 방향과 중력이 작용하는 방향은 수직이 된다. 이 때의 물체의 위치를 근일점이라고 부르고, 반대로, 중력체와 가장 멀리 떨어질 때, 속력이 최소가 되면서 속도의 방향과 중력의 방향이 수직인 위치를 원일점이라고 부른다.
지구를 포함한 거의 모든 행성이 타원궤도로 돌고 있으며, 주기혜성도 타원궤도로 돌고 있다. 주기혜성의 주기는 아주 길지만, 주기혜성을 관측할 수 있는 시간이 짧은 이유가 근일점에서 속력이 빨라지기 때문이다. 근일점에 있으면 태양빛이 세고, 원일점에 있으면 태양빛이 적어서, 지구의 여름은 근일점에 있을 때, 겨울은 원일점에 있을 때라고 생각할 수 있지만, 지구의 이심률은 꽤 작기 때문에 근일점과 원일점에 의해서 계절이 나타나는 것이 아니라, 지구의 자전축에 의해서 계절이 나타난다. 북반구와 남반구의 계절이 반대인 이유를 생각하면 유추하기 쉽다. 어느 한 항성계(태양계 등)에서 타원궤도를 가지는 천체들은 항성에 이끌려 있어 항성 주위를 돌게 된다.
쌍곡선 궤도
[+/-]쌍곡선 궤도도 타원 궤도와 마찬가지로 초점을 두 개 가지고 있다. 하나는 쌍곡선이 감싸고 있고, 다른 하나는 애니메이션에서 빨간색 점에 대해 초록색 선에 대칭한 위치에 놓여져 있다. 쌍곡선 궤도는 중력체가 지배적으로 중력을 행사할 수 있는 영역 밖에서 들어온 물체가 그리는 궤도이다. 외부에서 들어온 물체는 타원궤도와 마찬가지로 중력체와 가장 가까울 때 가장 큰 속력을 내며, 외부로 빠져나간다. 물체가 가지는 역학적 에너지가 중력에 의한 위치 에너지 차보다 크기 때문에 이런 궤도를 그린다.
쌍곡선 궤도는 오우무아무아 같은 외계천체나 스윙바이하는 탐사선에서 볼 수 있다. 탐사선의 경우, 탐사선이 가지고 있는 연료가 너무 적거나, 연료를 아끼거나, 시간을 아끼고 싶을 때 사용하는 방식으로, 주변 행성이나 왜소행성의 도움을 받아 속력을 뻥튀기 하거나, 줄이기 위해 사용한다. 탐사선이 도는 행성을 중심으로 바라봤을 때 쌍곡선 궤도를 그린다.
쌍곡선은 하나의 곡선을 의미하지 않는다. 쌍곡선의 초점을 설명한 것처럼 애니메이션에서 쌍곡선 궤도에 대하여 초록색 선에 대칭되게 하나의 곡선을 더 그릴 수 있는데, 이 곡선까지 더해서 쌍(雙)곡선이다. 중력은 끌어당기는 힘이지만, 만약에 중력과 같이 역제곱의 법칙을 따르면서 밀어내는 힘이 존재한다면, 원 궤도나 타원 궤도는 나오지 않을 것이다. 이 때는 쌍곡선 궤도만 존재하게 되는데 그 궤도가 중력에서 사용하지 않는 다른 쌍곡선이 그리는 궤도이다.
포물선 궤도
[+/-]포물선 궤도를 쌍곡선 궤도보다 나중에 설명하는 이유는, 원 궤도와 같이 자연에서 찾아보기 매우 힘든 궤도이기 때문이다. 존재하지 않는다고 봐도 무방할 정도로 포물선 궤도를 형성하는 것은 매우 어렵다. 포물선의 이심률은 1이라고 했는데, 타원 궤도와 원 궤도의 경우 항성에 이끌려 항성을 도는 궤도라고 했고, 쌍곡선 궤도는 외부에서 들어온 물체가 그리는 궤도라고 했다. 포물선 궤도는 타원 궤도도, 쌍곡선 궤도도 아닌 아주 절묘한 지점에서만 나타나는 궤도다. 이 궤도가 나타나기 위해서는 물체의 운동 에너지가 중력체에 의한 위치 에너지 차와 같아야 한다. 즉, 물체의 역학적 에너지가 항성계에 대해서 0이어야 한다.
포물선 궤도로 움직이는 물체는 없다고 봐도 무방하다. 온 우주에 중력체와 물체만이 존재한다고 가정했을 때, 포물선 궤도로 움직이는 물체는 무한대의 공간으로 나아가기 때문에, 실제 우주에서는 다른 중력권에 이끌려 궤도를 유지할 수 없다. 외부에서 궤도가 만들어질 때 역시 에너지가 한 치의 오차도 없이 딱 들어맞아야 하기 때문에 어거지로 만들지 않는 한 존재하지 않는다.
중력의 중심
[+/-]
위의 궤도의 설명의 경우 중력체를 고정시키고, 물체가 어떻게 움직이는지를 설명한 것이다. 실제로는 물체만 움직이는 것이 아니라, 중력체도 같이 움직인다. 물체의 궤도는 보는 시선에 따라 달리 보일 수 있다. 아주 단순하게, 위에서 설명한 것들은 물체를 고정시켜서 봐도 똑같이 원 궤도나 타원 궤도, 포물선 궤도나 쌍곡선 궤도로 움직인다.
더 넓은 시야에서 봤을 때, 원 궤도나 타원궤도에서 중력체와 물체는 어느 한 점을 기준으로 서로를 향해 돈다. 이 점을 우리는 질량 중심이라고 부른다. 태양계에서 질량중심은 태양 근처를 맴돌고 있다.
하나의 천체가 중력적으로 지배적인 공간에 존재하는 다른 천체에 비해 아주 크지 않는 경우, 질량 중심은 천체의 밖에 존재한다. 이 점을 중심으로 물체는 서로에게 똑같은 궤도를 가지며 움직인다. 그래서 쌍성을 관측할 때 두 개의 별이 하나의 점을 기준으로 돌고 있는 것처럼 보인다.
- ↑ 최대한 수식을 배재하면서 물리학을 서술하는 책은 많다.(천문학의 Horizons Exploring the Universe나 수학없는과학 등) 그러나 끝내 개념을 설명하기 위해 수식을 도입하거나, 수박 겉핥기식 개념서가 많은 것 뿐이다.
- ↑ The Event Horizon Telescope Collaboration et al. 2019. ApJL. 875 L1
- ↑ 아주 자주 청소년 필독 도서로 뽑힌다.
- ↑ 물리학자들의 작명 센스가 그렇듯이 말 그대로 초(Ultra) 고(High) 에너지(Energy) 우주(Cosmic) 입자(Ray는 X레이처럼 광선 등을 뜻하는 단어이지만, 알파선이나 베타선처럼 광자에 한해서 쓰이지 않는다.)이다. OMG 입자나 UHECR이나 감탄을 금치 못할 정도로 처참한 건 이미 유명하다.
- ↑ 유클리드라고 잘 알려져 있지만, 유클리드(Euclid)는 그리스인들의 이름을 라틴어화 하면서 생긴 이름이다. 유클리드보다 에우클레이데스라는 말로 쓴 이유는 아리스토텔레스(Ἀριστοτέλης)를 아리스토텔레(Aristotele)라고 쓰지 않는 것과 같다.
- ↑ 시간과 관련한 교양서적으로 카를로 로벨리의 《시간은 흐르지 않는다.》라는 책이 있다. 통계론적인 시간, 상대론적인 시간, 양자론적인 시간에 대해서 대중적인 수준(고등학교 재학생 수준)에서 다루고 있기 때문에, 관련된 쪽에 시간에 대한 이야기가 궁금하면 추천하는 책이다.
- ↑ 한국에서 출판된 서적은 《그래도 지구는 돈다》(교우사, 1997), 《대화 천동설과 지동설, 두 체계에 관하여》(사이언스북스, 2016)가 있다.
- ↑ 책은 대화 형식으로 되어 있고, 갈릴레이가 직접 말하는 것이 아니라, 등장인물의 입을 통해서 말한다.
- ↑ 빛이 일정하다는 가정은 그냥 갑자기 뿅하고 튀어나온 것이 아니다. 맥스웰의 방정식을 통해 유도된 연역적인 사실으로 아인슈타인의 상대성 이론이 갑자기 아인슈타인이 떠올린 사실은 아니다.
- ↑ 사실 이는 고대 중국의 춘추전국시대의 제자백가와 궤를 같이한다. (어떤 이유가 됐든 간에)학문적 자유가 학문적 발전으로 이어진다는 사실은 인류보편적이다.
- ↑ 남영 (2016년). 〈7장 뉴턴을 만든 세계, 과학단체의 출현〉, 《태양을 멈춘 사람들》. 궁리출판 [1]
- ↑ w:고전역학의 역사
- ↑ 이를 직관적으로 설명한 영상도 있다. [2]
- ↑ 당연히 현실에는 존재하지 않지만, 이에 가까운 w:밴타블랙이라고 하는 물질이 있다. 너무 반사율이 낮아서 밴타블랙으로 코팅된 물체를 보면 기이한 느낌이 든다.
- ↑ MIT 무료 강의(OCW) 중 Walter Lewin 교수가 턱에 진자 공을 대고 놓는 영상이 있다. Walter Lewin 교수의 유튜브 계정에 공개되어 있다.[3]
- ↑ 설명하는 유튜브 영상
- ↑ 아리스토텔레스가 정의한 시간의 정의다.
- ↑ I. Newton, 《NATURALIS PHILOSOPIÆ PRICIPIA MATHEMATICA》, "Lex. II. Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur."
- ↑ I. Newton, 《NATURALIS PHILOSOPIÆ PRICIPIA MATHEMATICA》, "Def. I. Quantitas Materiæ est mensura ejusdem orta ex illius Densitate & Magnitudine conjunctim."
- ↑ I. Newton, 《NATURALIS PHILOSOPIÆ PRICIPIA MATHEMATICA》, "Def. II. Quantitas motus est mensura ejusdem orta ex Velocitate et quantitate Materiæ conjunctim."
- ↑ 힘이라는 단어가 가진 의미가 다양하듯이, 크기라는 단어가 가진 의미도 다양하다. 정확히 무엇에 대해서 크고 작은 것인지가 정해져 있는 단어가 아니기 때문에, 크기로 무엇을 말하는 것 자체가 어렵다. 그러니까, 질량을 단순히 물질의 크기라고 정의했을 때, 그것의 부피가 큰 것인지, 밀도가 높은 것인지, 무거운 것인지를 제대로 지칭하지 못한다. 개인적으로 추측하건대 이런 말하기 어려운 고유한 값을 지칭하기 위해서 ~의 양이라는 표현을 쓴 것이 아닌가 싶다.
- ↑ 질량이 바뀌는 경우도 존재한다. 로켓이 발사되는 원리가 질량을 잃으면서 힘을 얻어내 나아가는 것이다.
- ↑ 망원경이 발명되기 전 이 7가지 행성과 위성, 항성은 점성술과 천문학(사실 잘 구분되지 않았다.)에서 중요한 천체들이었다.
- ↑ 충돌 실험만큼 자극적인 실험이 없기 때문에 각국의 교통안전국에서 벨트를 안 맨 상태에서의 충돌 실험 역시 진행했다. 호주 NSW(뉴사우스웨일스)주 정부에서 실험한 영상(두 번째 영상)
- ↑ 종단속력은 공기의 밀도에 영향을 받기 때문에 사실 대기가 희박한 곳에서 종단속력이 높아서, 대기가 상대적으로 희박한 높은 곳에서 더 많은 충격량을 받는다.
- ↑ 수학에서는 미분도 적분도 함수라고 부른다. 함수의 정의 자체가 입력값을 받아서 출력을 뱉어내는 것이기 때문에 잘 들어맞는 정의다.
- ↑ 이에 대해 수학계와 과학계에서 몇 백년간을 이어오는 떡밥이 있다. 라이프니츠와 뉴턴 중에서 누가 먼저 미적분을 발명했냐는 논쟁인데, 만들어진 건 언제나 뜨거운 감자지만, 미적분에 사용한 표기법만큼은 라이프니츠의 표기법이 주로 쓰인다.
- ↑ 동아사이언스 주말N수학 파이데이
- ↑ 리만 적분은 여기서 소개할 개념보다 더 자유로운 개념이다. 오른쪽 리만합, 왼쪽 리만합 같은 걸 굳이 생각하지 않아도 상관없고, 최대값, 최소값에 대해서 리만합을 잡아도 된다. 아니면 그냥 직사각형을 지나는 아무 점을 잡아서 리만합으로 삼아도 되고, 심지어 직사각형이 같은 너비를 가질 필요도 없다.
- ↑ w:en:Zeno's paradoxes
- ↑ 이것에 대한 이야기는 한국교육방송공사(EBS)의 다큐멘터리 '넘버스'에 나오는 내용과 유사함을 알려둔다.
- ↑ 순간이라는 표현에 시간이 들어있어서 이렇게 말하기에는 조금 어폐가 있는 감이 없지 않아 있지만, 시간에서 쓰이는 순간이라는 개념에서 '아주 조금'이라는 개념만을 뽑아서 쓰면 문제가 없다.
- ↑ 실제로는 주식은 전산화 되었고, 컴퓨터가 정보를 처리할 수 있는 시간단위가 있기 때문에 말도 안되게 작은 h를 상정할 수는 없다.
- ↑ 둘이 독자적으로 개발했기 때문에 누가 먼저냐를 놓고 아주 오랫동안 논쟁이 되어왔다.
- ↑ 그렇다. 이런 애매한 표현으로 200년 동안은 미분을 표현하였다.
- ↑ 변화가 없기 때문에 0일 수밖에 없다.
- ↑ 일반상대성이론에서는 부적절할 수 있는 표현이다. 질량이 없는 빛이 대표적인 예시다. 질량이 없는데 힘을 줘봤자 가속할리가 없지 않는가? 하지만, 빛은 중력에 의해서 경로가 휘는 것처럼 보인다.
- ↑ 2000년대 일본의 예능인 トリビアの泉(트리비아의 샘)에서 트럭에 피칭머신을 달아 검증한 적이 있다. 일본 공영방송 NHK에서 진행한 같은 실험
- ↑ 이를 w:무한소라고 한다.
- ↑ 적분은 정적분과 부정적분으로 나뉘어져 있는데, 이것은 미적분학에서 자세하게 다룬다.
- ↑ 이 뿐만이 아니라, 일어난 총에서 총알이 격발된 현상에서 시간을 거꾸로 돌려서 보면 발사된 총알이 총으로 돌아가는 것으로 기대하는 것을 시간 대칭성이라고 부른다. 이에 관한 내용은 최무영 서울대 물리천문학부 교수가 신문사 프레시안에서 연재한 [최무영의 '과학이야기'] 중 물리법칙의 대칭성(19, 20, 21) 혹은 이를 바탕으로 집필한 《최무영 교수의 물리이야기》에 더 자세하게 나와있다.
- ↑ 좀 더 엄밀하게는 힐베르트 공간에서 다룬다.
- ↑ 측정해주는 장치를 우리는 마이크라고 부른다.
- ↑ 삼각형에서 나온 함수인데 음수 각이 나오거나, 음수 값이 나오는 게 상식적으로 잘 받아들일 수 있는가?
- ↑ 아래 표를 위의 sine함수와 cosine함수가 나와있는 저 그림 위에 그려보자. 미분의 정의를 곱씹으면서 생각해보면 언제 올라가고 내려가는지에 대한 규칙을 찾을 수 있다.
- ↑ 이것을 활력(vis viva)라고 불렀다. 살아있는 힘 정도로 해석이 되는데, 에너지라는 개념 자체가 나중에 가서 정립되어서 그렇다.
- ↑ 물론 당구공은 잘 변형이 안되면서 잘 안 깨지는 방향으로 개발됐다. 조선일보, "[작지만 강하다]당구공 제조사 살뤽", 2000.4.20, 이광회 기자
- ↑ 뉴턴의 프린키피아에서 에테르에 대해 제대로 논하지 않고 있다. 뉴턴의 광학에서는 빛이 나아가기 위해선 매질이 존재해야 한다고 말하면서 에테르를 언급했다. 심지어 에테르의 밀도에 따라 빛이 굴절이 된다고 말하고 있다.
- ↑ 한국물리학회 용어집에서 trajectory를 궤적으로 번역, 한국천문학회에서는 trajectory를 궤도로 번역
- ↑ 영어로 가르칠 때는 orbit과 trajectory으로 구분한다. 두 개의 차이는 순환하는가의 여부이다. 다시 제자리로 돌아오는 경우 orbit이라고 하고, 돌아오지 않는 경우는 trajectory라고 부른다. 그래서 사실 원과 타원의 경우 orbit이지만, 포물선과 쌍곡선의 경우 trajectory이다. 한국어에서 orbit은 궤도로, trajectory는 궤적으로 번역하는 경우가 많지만, 궤도(軌道, 수레바퀴(혹은 기차바퀴)가 가는 길)와 궤적(軌跡, 수레바퀴(혹은 기차바퀴)가 간 흔적) 모두 돌다라는 의미를 가지고 있는 단어가 아니므로, 여기에서는 쌍곡선 trajectory도 쌍곡선 궤도라고 쓴다. 사실 궤적이라는 표현 자체가 과거를 내포하고 있기 때문에 좋은 번역어는 아니다.





















































































